Die Produktionsfunktion lautet, was ist richtg? mehrere Antwortmöglichkeiten sind möglich

Question

Die Produktionsfunktion eines Unternehmens laute

F( x1 , x2 )=69* (x1 ^0.15) *(x2^0.32) ,

wobei x1 und x2 die eingesetzten Mengen der beiden Produktionsfaktoren A und B bezeichnen. Die Kosten der Produktionsfaktoren betragen pro Mengeneinheit 9 bzw. 2 Geldeinheiten. Vom Endprodukt sollen 932 Mengeneinheiten gefertigt werden. Für die Produktionskosten in Abhängigkeit von den eingesetzten Mengen der beiden Produktionsfaktoren A und B existiert unter dieser Nebenbedingung im ersten Quadranten genau eine lokale Extremstelle. Markieren Sie die korrekten Aussagen.
a. Bei einem Output von 932 ME werden bei einer Menge von x1 =46.36 die Kosten minimal. b. Bei einem Output von 932 ME werden bei einer Menge von x2 =523.54 die Kosten minimal. c. Der Lagrange-Multiplikator im Kostenminimum beträgt λ=3.51. d. Das kostenminimale Faktoreinsatzverhältnis der beiden Produktionsfaktoren beträgt x1 x2 =0.09. e. Im Optimum betragen die Produktionskosten C( x1 , x2 )=1537.91.

Comments

Die Produktionsfunktion eines Unternehmens lautet, welche Aussage ist richtig?

---

Hast du die richtige Antwort gefunden ?

Answer 1

Da wird Lagrange insuniert (es ginge auch ohne).

Die Zielfunktion 9x₁ + 2x₂ (Minimum) und die Nebenbedingung 69 * (x₁^0.15) * (x₂^0.32) = 932 werden also umgeschrieben zu

9x₁ + 2x₂ + λ (69 x₁^0.15 x₂^0.32 - 932)

und das nach den drei Variablen abgeleitet und jeweils gleich Null gesetzt, was das behufs Finden des Optimums (Kostenminimums) zu lösende Gleichungssystem mit drei linearen Gleichungen und drei Unbekannten ergibt:

10.35 λ x₂^0.32/x₁^0.85 + 9 = 0
22.08 λ x₁^0.15/x₂^0.68 + 2 = 0
69 x₁^0.15 x₂^0.32 - 932 = 0

Aufgelöst ergibt das x₁ = 54.5357 und x₂ = 523.543 (und λ = -3.51088).

Wenn man Lagrange nicht verwenden wollen würde, kann man sich vergegenwärtigen, dass sich die Graphen der (linearen) Zielfunktion und der (nichtlinearen) Nebenbedingung beim Optimum berühren müssen (in der Graphik steht y anstatt x₂):

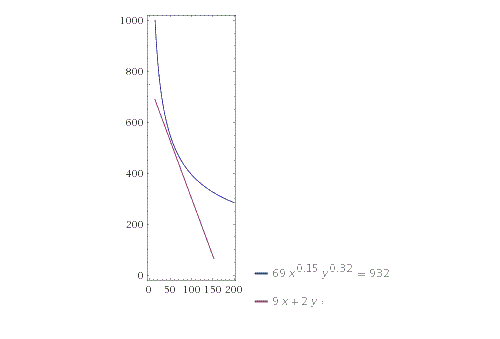
Das heisst, man löst die Nebenbedingung nach x₂ auf, setzt die erste Ableitung nach x₁ gleich -9/2 (der Steigung der Zielfunktion) und erhält so ebenfalls x₁ = 54.5357_.

Comments

Das Lustige dabei, Mathematica findet die Lösung nicht :)

Minimize[{9 x + 2 y, 69 x^0.15 y^0.32 == 932}, {x, y}]

kommt nicht zu einem Ende, und auch nicht die hilfreichere Formulierung zum Finden einer nur numerischen Lösung:

NMinimize[{9 x + 2 y, 69 x^0.15 y^0.32 == 932, {x, y} ∈ Reals}, {x, y}]

---

Kannst du mir weiterhelfen ?

---

Etwas war falsch

---

Bei der ersten Gleichung würde ich durch x₁^0.65 dividieren anstatt multiplizieren.

Bei der zweiten Gleichung fehlt der Faktor 15.39 und ich würde ebenfalls durch x₂^0.73 dividieren anstatt multiplizieren.

Bei der dritten Gleichung habe ich 57 anstatt 69.

---

Da haben wir es ja gleichzeitig bemerkt. Kommst du jetzt auf die Lösung?

---

Na ja , es dauert ein bißchen. Ich hoffe , dass ich lösen kann.

---

Wenn ich mich nicht verrechnet habe, ist in diesem Fall x₁=0.579592 und x₂=1.11778

---

Dann sind alle Aussagen falsch

---

Hast du denn dasselbe bekommen?

---

Nein ich könnte nicht

---

Die drei Gleichungen sind

19.95 λ x₂^0.27 / x₁^0.65 + 5 = 0

15.39 λ x₁^0.35 / x₂^0.73 + 2 = 0

57 x₁^0.35 x₂^0.27 - 952 = 0

und meine erste Lösung war offensichtlich falsch.

x₁ = 70.4663, x₂ = 135.899, λ = -1.05742

---

Ja ich habe auch Jetzt gefunden aber dann sind alle Aussagen falsch oder?

---

Wie kann ich die Produktionskosten finden ?

---

Die Formel steht im ersten Satz der Aufgabenstellung.

---

C(×1,×2)=57*70.4663^0.35*135.899^0.27

So?

---

Ja ich habe geschafft , nur c ist richtig. Danke für deine Hilfe @döschwo

---

Die Produktionsfunktion eines Unternehmens laute:

F(x,y)= 17 * (x^0,39) * (y^0,46)

wobei x1 und x2 die eingesetzten Mengen der beiden Produktionsfaktoren A und B bezeichnen. Die Kosten der Produktionsfaktoren betragen pro Mengeneinheit 7 bzw. 7 Geldeinheiten. Vom Endprodukt sollen 659 Mengeneinheiten gefertigt werden. Für die Produktionskosten in Abhängigkeit von den eingesetzten Mengen der beiden Produktionsfaktoren A und B existiert unter dieser Nebenbedingung im ersten Quadranten genau eine lokale Extremstelle. Markieren Sie die korrekten Aussagen.

a. Bei einem Output von 659 ME werden bei einer Menge von x1 =160.89 die Kosten minimal.
b. Bei einem Output von 659 ME werden bei einer Menge von x2 =79.73 die Kosten minimal.
c. Der Lagrange-Multiplikator im Kostenminimum beträgt λ=0.28.
d. Das kostenminimale Faktoreinsatzverhältnis der beiden Produktionsfaktoren beträgt x1 x2 =0.85.
e. Im Optimum betragen die Produktionskosten C( x1 , x2 )=1031.34.

---

Das löst du so wie das Beispiel weiter oben, aber mit deinen Zahlen anstatt den dort verwendeten Zahlen.