Reihe als Riemannsche Summe interpretieren um Grenzwert zu bestimmen

Question

Hey:)

Ich verstehe irgendwie nicht so ganz die Aufgabe. Soll ich mir irgendeine Funktion "aussuchen" und dann irgendein Intervall und davon die Riemann Summe berechnen?

Bestimmen Sie den Grenzwert
$$ \lim \limits_{n \rightarrow \infty} \sum \limits_{k=0}^{n} \frac{1}{n+k^{'}} $$
indem Sie \( \sum \limits_{k=0}^{n} \frac{1}{n+k} \) als die Riemannsche Summe einer geeigneten Funktion auf einem geeigneten Intervall auffassen. 

Reihe als Riemannsche Summe interpretieren um Grenzwert zu bestimmen 

Comments

Vielleicht \(f(x)=\large\tfrac1{1+x}\) im Intervall \(I=[0,1]\).

---

Und wie mach ich jetzt weiter? :)

---

ich weiß leider nicht, wie ich das zeigen soll. Könnt ihr mir bitte helfen?;)

---

Hab gerade durch einen Beitrag gesehen, dass es das gleiche wie ln2 ist, könnt ihr mir das zeigen?

---

Zerlege das Intervall \(I=[0,1]\) in \(n\) gleich große Teilintervalle. Die Untersumme berechnet sich aus$$U_n=\sum_{k=1}^n\tfrac1n\cdot f\left(\tfrac kn\right)=\sum_{k=1}^n\frac1n\cdot\frac1{1+\tfrac kn}=\sum_{k=1}^n\frac1{n+k}.$$

---

Ich versteh nicht so ganz deine Umformung. Woher kommt das k/n?

---

Das sind die Ränder der \(n\) gleich großen Teilintervalle \(I_k=\left[\frac{k-1}n,\frac kn\right], k=1,\dots,n\). Bei dieser Zerlegung hat ein typisches Rechteck der Untersumme die Breite \(\frac1n\), sowie die Höhe \(f\left(\frac kn\right)\).

---

Und für die Obersumme gilt das gleichen?

---

Die Obersummen lauten \(O_n=\sum\limits_{k=1}^n\frac1n\cdot f\left(\frac{k-1}n\right)\).

---

Woher kommt das k/n?

Wenn du das k/n nicht verstehst - es geht auch ohne.

Deine Summe ist 

  Σ [k=0 ... n] 1/ (n+k)

=  1/n  +  1/(n+1)  +  1/(n+2)  +  ...  +  1/(n+n)

=  1/n * 1  +  1/(n+1) * 1  +  1/(n+2) * 1  +  ...  +  1/(2n) * 1

Das sind alles Summanden der Form Höhe * Breite, wobei die Höhen 1/(n+k) alles y-Werte auf dem Graphen der Funktion  f  mit  f(x) = 1/x  zum x-Wert n+k sind und die Breiten alle 1 sind.

Es sind also genau die in der folgenden Skizze dargestellten Rechtecksflächen.

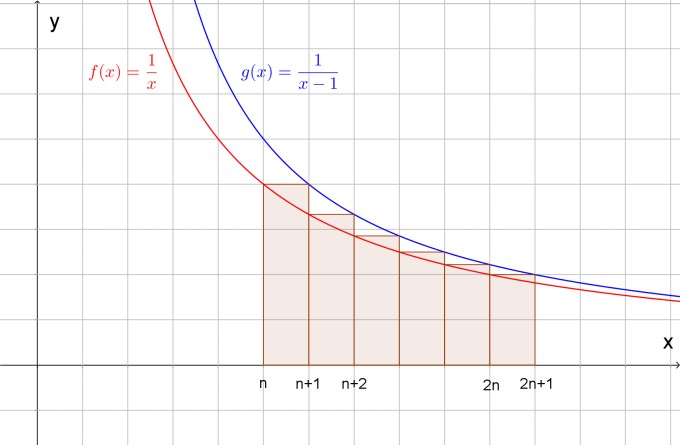
Sie stellen eine Obersumme zum Integral  ∫ [n .. 2n+1] f(x) dx  und auch eine Untersumme zum Integral   ∫ [n .. 2n+1] g(x) dx  dar.

Also ist

 ∫ [n .. 2n+1] f(x) dx  <  Σ ...  <  ∫ [n .. 2n+1] g(x) dx

⇔  ∫ [n .. 2n+1] 1/x dx  <  Σ ...  <  ∫ [n .. 2n+1] 1/(x-1) dx

⇔  ln x | [n .. 2n+1]  <  Σ ...  <  ln (x-1) | [n .. 2n+1]

⇔  ln (2n+1) - ln (n)  <  Σ ...  <  ln (2n) - ln (n-1)

⇔  ln ( (2n+1)/n )  <  Σ ...  <   ln ( 2n/(n-1) )

⇒ (lim [n → ∞] )    ln 2  ≤  Σ ...  ≤  ln 2  .

Answer 1

berechne nun nach dem Vorschlag von nn

$$ \int_{0}^{1}\frac { 1 }{ x+1 }dx=ln(2) $$

mithilfe des Hauptsatzes der Differential- und Integralrechnung.

Comments

Ich soll das aber mit Riemann zeigen

---

Mmmh also ich interpretiere die Aufgabe so:

gegeben ist die Riiemannsumme (erste Zeile).

Die sollst du aber nicht direkt ausrechnen, sondern dir überlegen zu welcher

Funktion mit Intervall diese gehört und dann darüber den Grenzwert  berechnen.

Ansonsten hat es ja gar keinen Sinn sich die Funktion zu überlegen ;)

---

Nee, anscheinend soll ich das mit der Riemann-Summe zeigen. Also 1/n ausklammern

Also ich muss das zeigen, was im Beitrag oben mit ln steht mit Riemann und später substituieren.

Nur irgendwie hilft mir das nicht weiter

---

Achso, du kannst ja auch eine andere Zerlegung des Intervalls nehmen und dann damit die Riemannsumme leichter explizit auflösen.

Kann ich dann später noch machen falls du da Hilfe brauchst ;)

---

Kannst du mir da vielleicht kurz helfen? Weil ich weiß nicht so recht, was ich machen soll...