Wieso hat die abschnittsweise definierte Funktion an diesen Stellen einen relativen Extrempunkt?

Question

aus den vorigen Teilaufgaben liegen folgende Werte vor:

G_f  ist streng monoton steigend für x ∈ [-ϖ ; 0] und [4; +ϖ]
G_f ist streng monoton fallend für x ∈ [ 0; 4]

f(x) = 1/6 x³ - x² 
f'(x) = 1/2 x² - 2x

WP f(x) = (2|-8/3)
TIP (4|-16/3)
HOP (0|0)

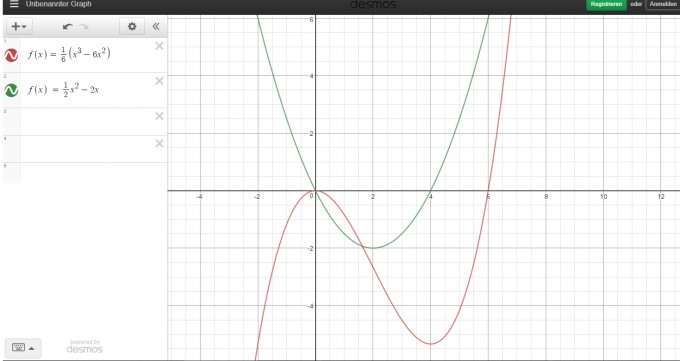
weiter ist die abschnittsweise Funktion h(x) gegeben:

h(x) = {(1/6) (x³ - 6x²) für x < 0
            (1/2)x² - 2x für x ≥ 0

Aufgabe 2.2 lautet nun: 
"Geben Sie die maximalen Monotonieintervalle sowie Art und Koordinaten sämtlicher Extrempunkte des Graphen der Funktion h an."

Die Monotonieintervalle habe ich bereits; die gehen aus Teilaufgabe 1.1 hervor.

Die Lösung sagt, dass der Hochpunkt von H (0|0) und der Tiefpunkt (2|-2) ist. Doch wie kann das sein? Der Graph hat schließlich Punkte, die tiefer bzw. höher liegen.

bis x=0 ist h(x) die Funktion f(x); ab x=0 ist es die Funktion der 1. Ableitung (im Bild grün).

Answer 1

Du sollst sämtliche Extrempunkte nennen. Dazu gehören auch lokale Extrempunkte. Bei (0|0) hast du ein lokales Maximum. Bei (2|-2) ist ein lokales Minimum.

Globale Maxima und Minima gibt es nicht, weil die Funktion nicht beschränkt ist.