Ellipse in 1. Hauptlage, wie Gleichung herausfinden?

Question

Wie rechnet man so etwas aus? 

Answer 1

Du fragtest: "Wie rechnet man so etwas aus?"

Du kannst z.B. bei Wikipedia nachschauen, was eine Ellipse ist. Und da hier kartesische Koordinaten vorliegen findest Du im Kapitel 'Ellipse in kartesischen Koordinaten' die Gleichung, die aus der Definition der Ellipse und dem Pythagoras folgt:

$$\sqrt{ (x - e)^2 + y^2 } + \sqrt{ (x + e)^2 + y^2 }=2a$$

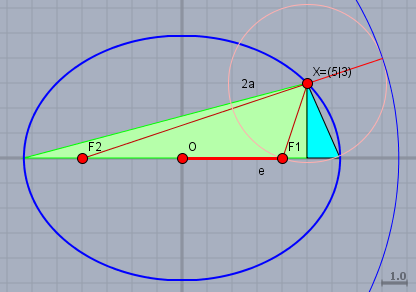
Jetzt noch die Zahlen aus der Aufgabenstellung einsetzen (\(x=5; \space y=3; \space e=4\)):

$$\sqrt{ (5 - 4)^2 + 3^2 } + \sqrt{ (5 + 4)^2 + 3^2 }=2a= \sqrt{10}+\sqrt{90}=4\sqrt{10} \space \Rightarrow a=2\sqrt{10} \approx 6,325$$

Die Ellipsengleichung findest Du dort auch:

$$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$$

Auflösen nach \(b^2\) und Einsetzen ergibt:

$$b^2=\frac{y^2 a^2}{a^2-x^2}=\frac{3^2 \cdot 40}{40 - 5^2}=24$$

Demnach lautet die Ellipsengleichung in a): $$\frac{x^2}{40} + \frac{y^2}{24}=1$$ und b) schaffst Du jetzt alleine; ansonsten frage nochmal nach.

Answer 2

a)

√((x - e)^2 + y^2) + √((x + e)^2 + y^2) = 2·a

√((5 - 4)^2 + 3^2) + √((5 + 4)^2 + 3^2) = 2·a --> a = 2·√10

 

b^2 = a^2 - e^2

b^2 = (2·√10)^2 - 4^2 --> b = 2·√6

 

x^2/a^2 + y^2/b^2 = 1

x^2/40 + y^2/24 = 1

 

b)

√((x - e)^2 + y^2) + √((x + e)^2 + y^2) = 2·a

√((3 - 4)^2 + 1^2) + √((3 + 4)^2 + 1^2) = 2·a --> a = 3·√2

 

b^2 = a^2 - e^2

b^2 = (3·√2)^2 - 4^2 --> b = √2

 

x^2/a^2 + y^2/b^2 = 1

x^2/18 + y^2/2 = 1

 

Answer 3

Schau mal dort

https://www.mathelounge.de/450053/ellipse-in-1-hauptlage-wie-gleichung-herausfinden

und verwende 

x² / a² + y² / b² = 1          und  e² = a² - b²

setze alles ein  und berechne a und b

25 / a² + 9/ b² = 1          und  16= a² - b²   


25  + 9a²/ b² =a²          und   b²    = a²  -16

25  + 9a²/ (a²  -16)  =a²   

jetzt substituieren  z = a² 

gibt    25  + 9z/ (z  -16)  = z

<=>   25(z-16)   + 9z  = z (z-16)

gibt z = 40 oder z=10

weil aber z≥16 sein muss nur  z= 40

also a² = 40 und b² = 24

Ellipse:    x² / 40  + y² /24 = 1