Das der rote Winkel bei \(P\) in der Skizze oben \(=\pi-2\alpha\) ist, hatte ich auch schnell gemerkt; aber es auch zu beweisen war dann doch schwieriger ... man sehe sich folgende Skizze an:
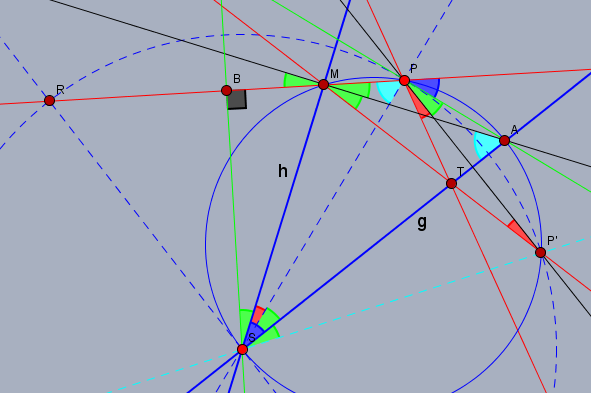
Der grüne Winkel \(PSA\) bei \(S\) sei \(\varphi\) und der blaue Winkel bei \(S\) ist das \(\alpha\) aus der Aufgabenstellung. Da das Dreieck \(SMB\) rechtwinklig ist mit dem Winkel \(\varphi\) bei \(S\), taucht \(\varphi\) auch im Punkt \(M\) auf, da die schwarze Gerade durch \(M\) die Orthogonale auf \(h\) ist. Demnach ist auch der Scheitelwinkel \(PMA=\varphi\) und da die Gerade durch \(MT\) das Spiegelbild von der Geraden durch \(PR\) ist, ist auch der Winkel \(AMT=\varphi\). \(A\) sei der Schnittpunktpunkt der Orthogonalen zu \(h\) mit \(g\). \(P'\) ist das Spiegelbild von \(P\) an \(g\) und da der Winkel \(PMP'=2 \varphi\) gleich dem Winkel \(PSP'=2\varphi\) ist, müssen die Punkte \(S\), \(M\), \(P\) und \(P'\) auf einem Kreis liegen. Auf Grund der Symmetrie liegt der Durchmesser auf der Geraden durch \(SA\). Und weil \(AMS\) ein rechter Winkel ist, liegt auch \(A\) auf diesem (Thales)Kreis.
Jetzt kann man mit Hilfe der Peripheriewinkel zeigen, dass alle Winkel gleicher Farbe auch gleich groß sind. \(\varphi\) findet man auch im Punkt \(P\) über den Vergleich der Winkel \(ASP'\) und \(APP'\). Den roten Winkel \(\alpha-\varphi\) findet man ebenso bei \(P\) bzw. \(P'\) über den Vergleich von \(MSP\) und \(MP'P\). Der hellblaue Winkel \(SAM\) bei \(A\) ist \(\pi/2-\alpha\), da das Dreieck \(SMA\) ein rechtwinkliges ist. Diesen Winkel findet man wieder bei \(SPM\). Und da der Winkel \(APS\) ein rechter ist, so ist der blaue Winkel bei \(P\)
$$\pi - (\frac{\pi}{2}-\alpha) - \frac{\pi}{2}=\alpha$$
und ein blauer \(\alpha\) ein grüner \(\varphi\) und eine roter \(\alpha-\varphi\) ergeben zusammen
$$\alpha + \varphi + \alpha - \varphi = 2 \alpha$$
Gruß Werner