Das lässt sich gut am Einheitskreis zeigen:
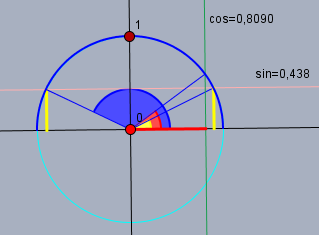
Es sind nur Winkel im Bereich \((1°;180°)\) gesucht. Also oben im Bild nur auf dem blauen Kreisbogen. Zeichnet man nun eine Waagerechte im Abstand von 0,4384 (die rosa Gerade), so schneidet diese den erwähnten Kreisbogen an zwei Stellen. Nämlich bei den Winkeln \(26°\) (gelb) und \(154°\) (blau). Den Sinuswert dieser Winkel kann man an den gelben Srrecken ablesen.
Um den Winkel \(\alpha\) zu finden, für den \(\cos \alpha = 0,8090\) gilt, zeichnet man eine Senkrechte (grün) im Abstand von 0,809 von der vertikalen Achse. Diese schneidet den blauen Kreisbogen nur einmal. Beim Winkel von \(36°\) (rot). Die rote Strecke auf der horizontalen Achse ist der Cosinus dieses Winkels.