Steigung berechnen bei Polarkoordinaten

Question

Ich habe eine Funktion r(φ) in Polarkoordinaten gegeben mit r(φ) = φ² 

Die x - y - Koordinaten an der Stelle φ = π/5 konnte ich bereits berechnen:

x = 0,3194

y = 0,2320

Jetzt soll ich den Anstieg der Kurve dy/dx an der Stelle φ = π/5 berechnen.

Ich wollte zunächst so vorgehen, dass ich hier einfach die Steigung m mit y/x berechne. Aber das funktioniert hier nicht. Könntet ihr mir bitte hier auch nochmal helfen?

Answer 1

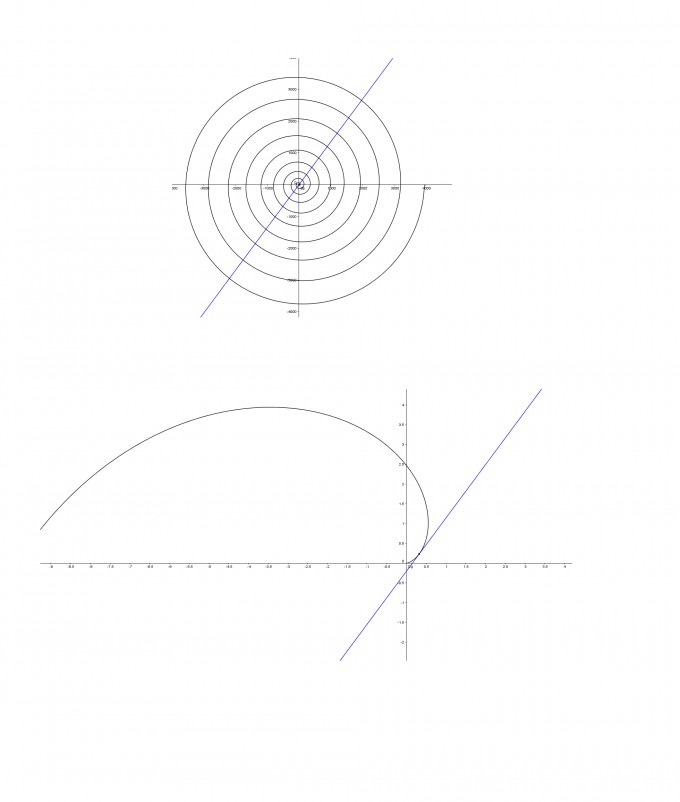
r(φ) = φ²
dr/dφ = 2φ

y = f(x(φ))

Kettenregel:
dy/dφ = dy/dx * dx/dφ

Umstellen nach dy/dx:
dy/dx = (dy/dφ)/(dx/dφ)

y = y(φ) = r(φ)sin(φ)
x = x(φ) = r(φ)cos(φ)

Produktregel:
dy/dφ = dr/dφ sin(φ) + r(φ) cos(φ)
dx/dφ = dr/dφ cos(φ) - r(φ) sin(φ)

dy/dx = (dy/dφ)/(dx/dφi) = [dr/dφ sin(φ) + r(φ) cos(φ)] / [dr/dφ cos(φ) - r(φ) sin(φ)]
dy/dx = (dy/dφ)/(dx/dφi) = [2φ sin(φ) + φ² cos(φ)] / [2φ cos(φ) - φ² sin(φ)]

φ=π/5, r(φ) = φ² = (π/5)²
 
dy/dx = (dy/dφ)/(dx/dφi)

= [2(π/5) sin(π/5) + (π/5)² cos(π/5)] / [2(π/5) cos(π/5) - (π/5)² sin(π/5)] ≈ 1.348

≈ 54,07 Grad