Ich bereite mich gerade auf eine Klausur vor und eine Übungsaufgabe aus dem letzten Jahr war die Kardinalität der folgenden Menge zu bestimmen:
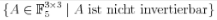
Ich weiß zwar, dass die Lösung 465125 ist, aber ich komme beim besten Willen nicht drauf wieso. Eine Matrix ist nicht invertierbar, wenn ihre Determinante = 0 ist bzw. wenn sie nicht vollen Rang hat. Da wir Determinanten zu dem Zeitpunkt der Übung noch nicht hatten, war mein Gedanke es über den Rang zu versuchen. Ich müsste also doch eigentlich die Anzahl der 3x3 Matrizen mit Rang 2 + die Anzahl der 3x3 Matrizen mit Rang 1 in F5 (endlicher Körper mit 5 Elementen) bestimmen. Soweit mein Ansatz, allerdings weiß ich nicht genau wie ich das anstelle. Meine bisherigen Versuche lieferten ständig falsche Ergebnisse und ich bin mit meinem Latein langsam am Ende. Kann mir vielleicht jemand auf die Sprünge helfen?