Wahrscheinlichkeitsrechnung Normalverteilung

Question

Wie groß ist die Wahrscheinlichkeit (zwischen 0 und 1), dass eine standardnormalverteilte Zufallsvariable kleiner als z= 2.34 ist?

Lösung kaufmännisch auf vier Nachkommastellen gerundet an.

Was ist der gesuchte Wert?

Answer 1

Φ(2.34) = 0.9903581300

Comments

Φ(2.34) ≅ 0.9903581301

---

danke für die Antwort kann mir aber jemand das vielleicht erklären ? :)

---

Betrachte die Standardnormalverteilung:

 

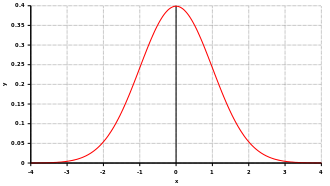
Das unter der roten Kurve ist die Wahrscheinlichkeit und hat den Flächeninhalt 1 (mit 100% Wahrscheinlichkeit passiert irgendetwas). Das unter der Kurve links von Null hat den Flächeninhalt 0,5 (mit 50% Wahrscheinlichkeit ist der Wert kleiner als Null), das rechts davon ebenfalls.

Die Wahrscheinlichkeitsdichte (Höhe der roten Linie) hat die Formel

und ihr Integral (Flächeninhalt von ganz links bis zum Wert x) hat die Formel

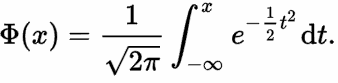
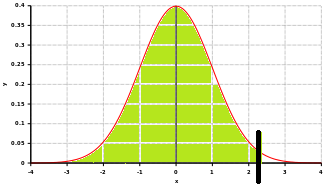
Gesucht ist nun der Wert von Φ (Flächeninhalt) bei x = 2,34.

---

Kannst du vielleicht alle Schritte aufzeigen ?

---

Nun du integrierst die Formel die über der grün angemalten Grafik steht, bis x = 2.34 und kommst als Lösung auf die weiter oben angegebenen ca. 99 %.

Das ist sowohl das Integral unter der roten Kurve bis 2.34 (der dicke schwarze Strich) wie auch der Inhalt der grün angemalten Fläche wie auch die gesuchte Wahrscheinlichkeit.

---

Wie integriere ich den Bis 2,43 ?

---

Ach man kann den Wert doch einfach von der Tabelle ablesen oder nicht

---

Für die Standardnormalverteilung gibt es dazu Tabellen, ja.