Integralrechnung , Bestimmung der Variabel a

Question

Für welchen Wert von a schliessen die Graphen der Funktion

f1: y=ax und f2: y= x^2-ax  eine Fläche von Inhalt A=36 ein?

Answer 1

Die beiden Funktionen schneiden sich offensichtlich bei 0 und bei 2a. Dann ergibt sich:

Comments

a kann auch eine negative Zahl sein. Dann hat das Integral umgekehrte Grenzen.

---

Yep, Tante Eusebia naht schon mit dem Nudelholz.

---

...schaut dann so aus:

Answer 2

Hallo IE,

die Schnittstellen der beiden Funktionen ergeben sich aus

x² -  ax  =  ax

x² - 2ax = 0

x * (x - 2a) = 0

x₁ = 0  ,  x₂ = 2a

A = | ₀∫^2a (f(x) - g(x)) dx | = | ₀∫^2a ( x² - 2ax ) dx |  = |  [1/3 x³ - ax² ]₀^2a |

                                           =  |  8/3 a³ - 4/3 a³ |  = | 4/3 a³ |

 | 4/3 a³ |  36  ⇔   4/3 a³    = ± 36   ⇔  a³ = ±27

→_in ℝ      a₁  = 3  ,  a₂ = -3  

Für a=3  ( für a = -3 spiegelt sich alles an der y-Achse) :

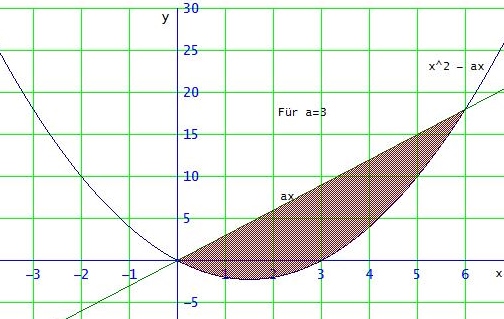
Gruß Wolfgang