2. partielle Ableitung berechnen und Frage zur Notation. f_(x)(2,1) = 3

Question

Hallo liebe Mathefreunde,

folgende Aufgabe ist gegeben:

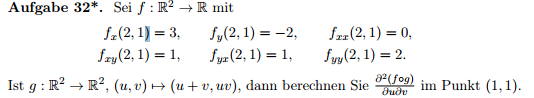
Meine Frage hierzu (Bitte keine Musterlösung geben, will selbst drauf kommen :) )

1. Was genau bedeutet überhaupt die Notation f_x,f_xy, etc.? Sind das die partiellen Ableitungen von f bloß in kurz geschrieben?

2. Wie genau starte ich bei der Aufgabe?

Falls meine Vermutung unter 1. richtig ist, würde ich mir versuchen eine Funktion f zu basteln, für die alle diese partiellen Ableitungen so passen, und dann kann ich ja einfach die beiden Ableitungen der Kompositionen berechnen.

3. Wie suche ich mir diese Funktion f?

Comments

zur Schreibkonvention:

$$ f=z(x,y)$$

$$ f_x=\frac{  \partial    z}{   \partial   x} $$
$$ f_y=\frac{  \partial    z}{  \partial   y} $$
$$ f_{xx}=\frac{  \partial   ^2 z}{  \partial   x   \partial   x} $$
$$ f_{yx}=\frac{  \partial   ^2z}{  \partial   y   \partial   x} $$

etc.

EDIT:

habe die "d" durch  " \partial "   ersetzt.

bitte die Schlamperei zu entschuldigen

---

Als Ansatz könnte man vielleicht mal
$$z(x,y)=ax^2+bx+cxy+dy+ey^2+f$$
versuchen - es könnte aber auch eine andere Funktion zugrundeliegen ...

---

Damit sind ja die partiellen Ableitungen gemeint oder? Ich verstehe noch nicht so ganz wann man d und wann man d mit dem Schwung benutzt...

Danke schon mal für die Hilfe :)

---

Ich verstehe noch nicht so ganz wann man d und wann man d mit dem Schwung benutzt...

Dazu hattest Du doch schon zwei Threads. Was willst Du denn noch alles wissen, was da nicht schon zur Sprache kam?

---

"   \partial   "

$$  \partial  $$ wird benutzt, wenn nach mehreren Variablen abgeleitet wird.

Das ist Schreibkonvention, da es auch Funktionen gibt, die jede Menge Parameter haben, nach denen nicht abgeleitet werden soll - dort nimmt man das "gerade" kleine "d" , wenn nur nach einer Variablen abgeleitet wird.

Für die Lösung der obigen Aufgabenstellung ist das allerdings nicht wirklich relevant, ob 'd' gerade oder gebogen ist - das Problem liegt woanders.

---

Jetzt hast Du mindestens drei Antworten auf einen unwichtigen Teil der Aufgabe bekommen - willst Du Dich nicht mal mit dem Kern der Aufgabe etwas befassen ?

---

Gern, wo genau liegt der Kern der Aufgabe? Eigentlich ja das "Basteln" der Funktion f(x,y)...

Sorry Fakename, nicht jeder denkt so schnell :)

---

Ich hab ja mal oben bereits einen möglichen Ansatz vermutet - nun bilde davon die entsprechenden Ableitungen und ...

---

\(f\) soll (und kann) nicht erraten werden. Ich fang mal an: $$\frac{\partial}{\partial u}f(u+v,uv)=f_x(u+v,uv)+vf_y(u+v,uv).$$ Und jetzt das noch nach \(v\) ableiten und dann bemerken, dass \(1+1=2\) und \(1\cdot1=1\).

---

Hmm..., so ganz verstehe ich das nicht.

Dein Anfang bedeutet ja, dass wenn ich f nach u ableite, ist es das selbe als wenn ich f nach x (Ist das in diesem fall dann u+v?) ableite und v • f nach y (also u*v?) ableite, oder wie?

Danke für deinen Ansatz!