gebrochen-rationale Funktion y=f(x) mit den folgenden Eigenschaften

Question

 Bestimmen Sie eine gebrochen-rationale Funktion y=f(x) mit den folgenden Eigenschaften

: Die Funktion hat Nullstellen bei x=1 und x=2 und die Gerade y=3 als Asymptote und es gilt: f(4)=1. Die Funktion hat aber keine Polstellen! Bestimmen Sie eine Funktionsgleichung. 

Tipp: Funktionen der Gestalt f(x)=x^2+a  , f(x) =x^4+a , f(x)= x^6+a  haben für a>0 keine Nullstellen.

Answer 1

Hallo HJ,

wegen der Nullstellen, der Asymptote 3 und der fehlenden Polstellen ist der einfachste Ansatz

f(x) = 3 *(x-1) * (x-2) / (x² + a²)   (der Summand soll positiv sein, da keine Polstellen)   

f(4) = 1  →   a = ±√2     ;  keine Polstellen   →  a = √2 

f(x)  =  3 *(x-1) *(x-2) / (x² + 2) 

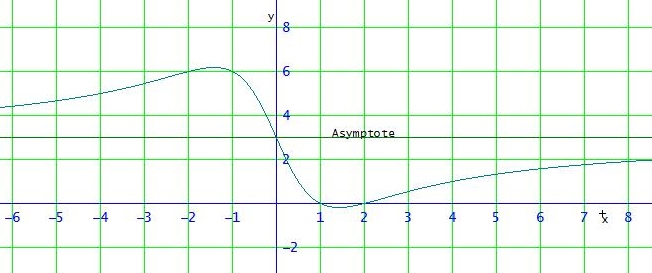
Gruß Wolfgang

P.S.  Das war jetzt meine vierte Antwort ohne jede Reaktion von dir. Wenn du dich schon nicht anmeldest und deshalb nicht kommentieren kannst, kannst du wenigstens mal auf den Daumen und/oder oben rechts auf "Beste" drücken.

Comments

Mach dir nichts draus das scheint ein Student von meiner Uni zu sein der in der Mathe-Übungsgruppe Zusatzpunkte abstauben will ohne selbst was dafür zu tun. Ich sitze grade vor den selben Aufgaben und bin dir sehr dankbar für deine Lösungen, denn mit den Vorlesungsunterlagen allein kommt man leider nicht weit wenn man nicht gerade extrem begabt in Sachen Mathe ist. ;)

MfG