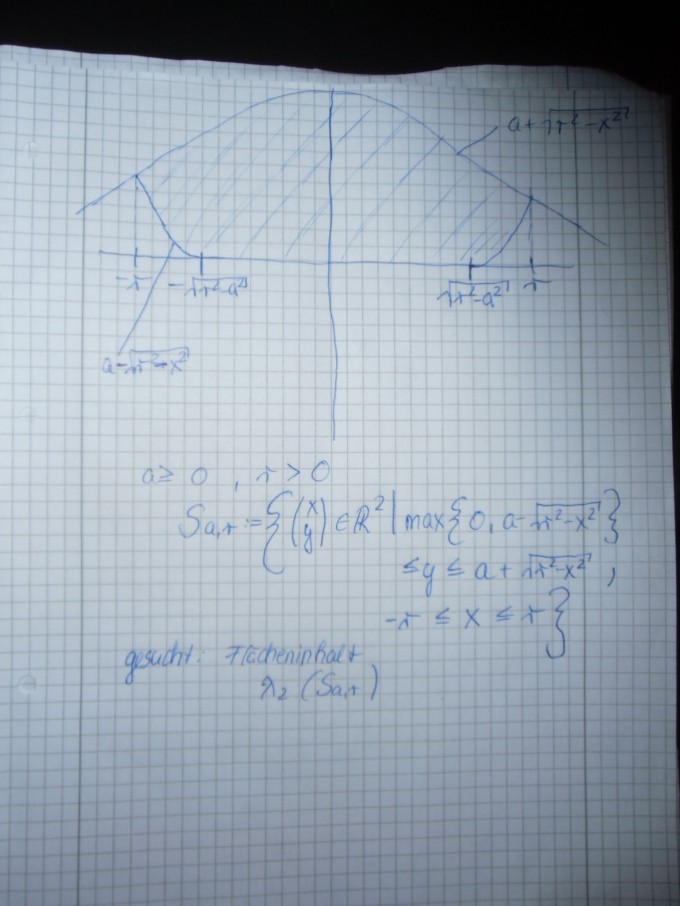
Folgende Aufgabe:
Berechnen Sie den Flächeninhalt λ2 (Sa , r)
mit Sa , r := { (x,y) ∈R² | max { 0 , a - √(r²-x²) } ≤ y ≤ a + √(r²-x²) , -r ≤ x ≤ r
mit a ≥ 0 und r > 0
Ich habe es gezeichnet hoffe es ist richtig. Meine Frage ist Muss man die beiden Seitenteile , also zB das rechte Seitenteil mit
$$ \int_{\sqrt { r² - a² }}^{r} a - \sqrt { r² - x² } dx $$ (wegen Symmetrie das doppelte davon)
von
$$\int_{-r}^{r} a + \sqrt { r² - x² } dx$$ abziehen?
Oder wäre es möglich es gleich voneinander abzuziehen , also f(x) - g(x) :
$$\int_{-r}^{r} (f(x) - g(x)) dx =\int_{-r}^{r} (a + \sqrt { r² - x² } - (a - \sqrt { r² - x² }))dx= 2 \int_{-r}^{r} \sqrt { r² - x² } dx$$