Frage zur Integralrechnung + Flächenbilanz

Question

ich habe zwei funktionen die sich schneiden  1/2x^4 - 5/2x^2+2 = x^2-1.  Das Intervall hat die Grenzen x1=-1 und x2=x1. ein teil der fläche die von der funktion eingeschlossen wird befindet sich unterhalb der x achse. sind aber dennoch achsensymmetrisch. spricht man in diesem fall trotzdem von einer flächenbilanz?

wäre nett wenn mir einer helfen könnte und danke im voraus.

Comments

Was soll denn x2=x1 heißen?

Answer 1

Hallo Code1234! :-)

"spricht man in diesem fall trotzdem von einer flächenbilanz?"

Wenn Du die Fläche zwischen den Funktionen im Intervall [-1, 1] meinst, dann nein.
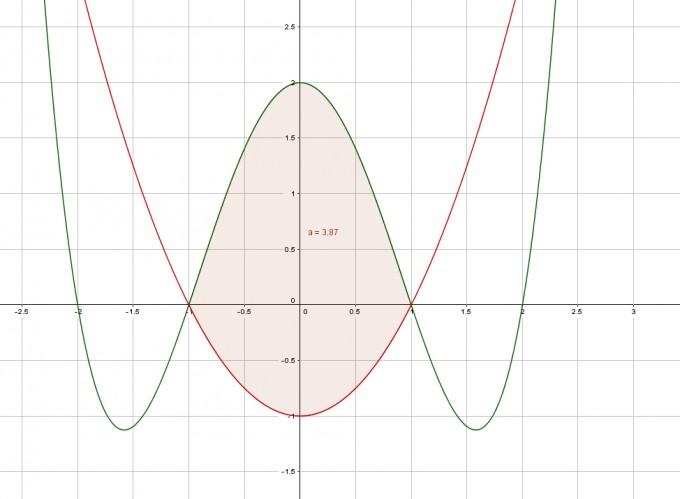
Die Formel zur Berechnung der Fläche, die von den Funktionen f, g zwischen zwei benachbarten Schnittpunkten a, b eingeschlossen ist, ist: | _a∫^b(f(x) − g(x))dx |

Mit f(x) = 1/2 x^4 - 5/2 x^2 + 2 und g(x) = x^2 - 1 ist  | _-1∫¹ (1/2 x^4 - 5/2 x^2 + 2 - (x^2 - 1)) dx | = 3,87

Die Fläche von f(x) oberhalb der x-Achse im Intervall [-1, 1] ist größer als die Fläche von g(x) in demselben Intervall.
Mit Flächenbilanz könnte gemeint sein:  _-1∫¹(f(x) + g(x)) dx  = 1,2

Beste Grüße
gorgar