Deine Zeichnung ist nicht ganz richtig. Es ist folgenderweise: 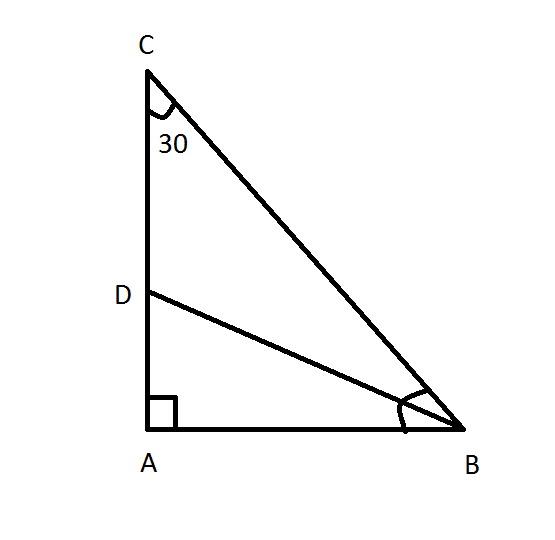
Da der Winkel A gleich 90 Grad und C gleich 30 Grad ist, bekommen wir dass B gleich 180-(90+30) = 180-120 = 60 Grad ist.
Vom Sinussatz beim Dreieck ABC haben wir folgendes: $$\frac{\sin C}{AB}=\frac{\sin B}{AC} \Rightarrow \frac{\sin 30^{\circ}}{AB}=\frac{\sin 60^{\circ}}{AC} \Rightarrow \frac{\frac{1}{2}}{\sqrt{3}}=\frac{\frac{\sqrt{3}}{2}}{AC} \Rightarrow \frac{1}{2\sqrt{3}}=\frac{\sqrt{3}}{2\cdot AC} \Rightarrow AC=3$$
Vom Sinussatz beim Dreieck BDC bekommen wir folgendes: $$\frac{\sin \frac{B}{2}}{DC}=\frac{\sin C}{BD} \Rightarrow \frac{\sin 30^{\circ}}{DC}=\frac{\sin 30^{\circ}}{BD} \Rightarrow BD=DC$$
Vom Sinusstz beim Dreieck ABD bekommen wir folgendes: $$\frac{\sin \frac{B}{2}}{AD}=\frac{\sin A}{BD} \Rightarrow \frac{\sin 30^{\circ}}{AC-DC}=\frac{\sin 90^{\circ}}{DC} \\ \Rightarrow \frac{\frac{1}{2}}{3-DC}=\frac{1}{DC} \Rightarrow \frac{1}{6-2DC}=\frac{1}{DC} \\ \Rightarrow 6-2DC=DC \Rightarrow 3DC=6 \Rightarrow DC=2$$
ODER:
Wir haben folgendes $$\tan(ABC)=\frac1{\sqrt3}=\frac{CD}{\sqrt3}\Rightarrow CD=1 \\ \tan(ABD)=\sqrt3=\frac{DA}{\sqrt3}\Rightarrow DA=3$$
Also haben wir dass $$CD=CA-DA=2$$