Erklärung von Begriffen zum Thema FUNKTIONEN

Question

es wäre sehr lieb wenn ihr mir etwas behilflich sein könntet ....

 

Was ist eine Definitionsmenge bzw. ein Definitionsbereich der Funktion f ?

Was ist mit Wertemenge gemeint ?

Was ist ein Funktionsterm ?

Wie kann man eine Funktionsgleichung definieren ?

 

Ich habe schon lange im Internet gesucht, bislang noch keine Seite gefunden, wo es leicht verständlich erklärt wird .

 

Danke für eure Hilfe !

Answer 1

Hi,

eine Funktionsgleichung ist das komplette.

Nehmen wir uns mal die Funktionsgleichung

f(x) = 1/(x-2) als Beispiel

 

Funktionsgleichung: f(x) = 1/(x-2)

Funktionsterm: 1/(x-2)

dabei ist "Term" ein anderes Wort für "Ausdruck".

 

Für die Defintionsmenge gilt der Spruch "Was kann x alles sein".

Bedenke hierbei beispielsweise, dass der Nenner nicht 0 werden darf. In unserem Falle ist also x=2 nicht erlaubt! Die Definitionsmenge deshalb x∈ℝ\{2} (also alle reelle Zahlen außer/ohne die 2).

 

Wertemenge:

Was kann f(x) = y alles sein. Da f(x) = 1/(x-2) von -∞ nach +∞ läuft, ist die Wertemenge alles außer y=0. Dieser Wert kann nie erreicht werden -> Es gibt keine Nullstelle.

 

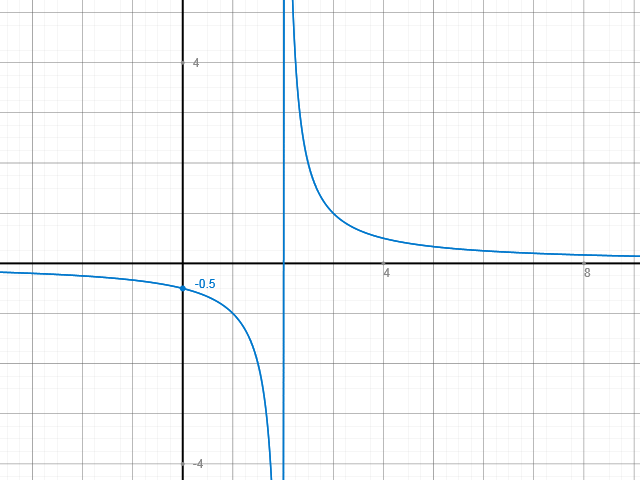
Definitionsmenge und Wertemenge können auch am Schaubild erkannt werden. Siehst Du es?

Grüße

Comments

Danke für deine so ausführliche Antwort, aber ich kann dir gar nicht folgen.

---

Kannst Du mir sagen, wo ich die abgehängt habe?

Ich habe ja eigentlich die Begriffe in andere Worte gefasst und ein Beispiel gegeben ;).

---

Ich habe noch nicht so viel mit Funktionen zu tun gehabt und deswegen verstehe ich nicht soviel davon.
Z.B. bei Definitionsmenge schreibst du  etwas von  x∈ℝ\{2} .... Da weiß ich gar nicht was das ist ....

---

Oh, dann seit ihr noch nicht soweit, wie ich vermute.

Dann wird es natürlich schwer mit dem Erklären. Dann lass mal mein Beispiel weg und orientiere Dich an meinen Worten.

 

Defintionsmenge: "Was darf x sein".

Wertemenge: "Was kann y sein".

---

Es tut mir sehr leid ich weiß nicht so recht was du mit deinen Worten meinst.
Trotzdem danke das du dich so viel damit beschäftigst   :)

---

Hmm,

ich würde eben doch gerne ein Beispiel nehmen.

Eben obiges, wo man direkt schon ein Schaubild hat, also f(x) = 1/(x-2)

 

Die siehst doch oben im Schaubild, dass die Kurve von links nach rechts geht. Die einzig "komische" Stelle ist doch bei x=2. Hier haben wir einen senkrechten Strich, welcher nicht erlaubt ist. Eben das wird durch die Definitionsmenge beschrieben. Diese sagt aus "x=2 darf nicht sein!, alles andere ist erlaubt".

 

Ich gehe richtig in der Annahme, dass Dir "Polstelle" als Begriff unbekannt ist? :P

 

Es tut mir leid, aber eine andere Idee das näher zu bringen habe ich nicht :/.

---

ist das bei x = 2 kein scheitelpunkt ?

---

Ein "Scheitelpunkt" ist der tiefste/höchste Punkt einer Parabel. Das liegt hier nicht vor ;).

---

@Gast: Schau dir bitte alle Videos zu den Funktionen an, beginnend bei F01, F02, ... https://www.matheretter.de/mathe-videos#fkt

Die Erklärung in Unknowns Antwort ist sehr gut und leicht zu verstehen, wenn du das Wissen aus den Videos kennengelernt hast.