Kann mir einer schnell sagen welche Regeln hier verwendet werden: Konvergenzradien Potenzreihe

Question

kann mir bitte einer schnell nennen mit welcher Regel ich das berechnen soll?
Was muss ich machen? Oder kann mir einer das zeigen wie das gemacht wird?

Comments

Vom Duplikat:

Titel: Konvergenzradien der Potenzreihe bitte mit Erklärung

Stichworte: konvergenzradius,potenzreihe,konvergenz

ich habe folgende Aufgabe und möchte gerne wissen was gemacht werden soll.

Ich möchte gerne wissen was Konvergenzradien sind. Brauche eine einfache Erklärung. Bin nicht fündig geworden bzw. nicht verstanden.

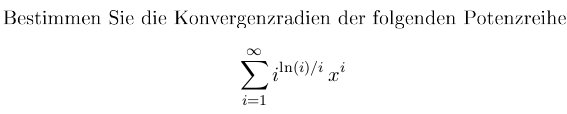
Wenn ich das richtig verstanden habe, handelt es sich um eine Summe von i=1 bis unendlich:

1^ln(1)/1 * x¹ + 2^ln(2)/2 *x² + ...

Aber wie berechne ich das jetzt? Vielen Dank für jegliche Hilfe.

---

Irgendeiner eine Idee?

---

Gibt es eine einfache Anleitung?

---

Komme einfach nicht weiter. Welche Regel soll man anwenden? Cauchy-Hadamard? Ich komme damit auch nicht weiter. Kann mir das irgendeiner vorrechnen?

Answer 1

Cauchy-Hadamard geht immer zur Berechnung des Konvergenzradius.

Bsp:

a)

$$ r=\frac { 1 }{ \lim_{i\to\infty}sup(|{ a }_{ i }|^{1/i}) }\\ $$

Es bleibt also zu berechnen:

$$  \lim_{i\to\infty}sup(|{ a }_{ i }|^{1/i}) \\=\lim_{i\to\infty}sup(i^{ln(i)/i})^{1/i}\\=\lim_{i\to\infty}sup(i^{ln(i)/i^2})\\=\lim_{i\to\infty}i^{ln(i)/i^2}\\=\lim_{i\to\infty}e^{ln[i^{ln(i)/i^2}]}\\=\lim_{i\to\infty}e^{ln^2(i)/i^2}\\=\lim_{i\to\infty}e^{(ln(i)/i)^2}\\=e^0=1\\\to r=1 $$

bei b) bietet sich das Quotientenkriterium an

unb bei c) musst du zuerstmal die innere Summe ausrechnen

Comments

Bei c habe ich

$$\frac{ln(1-x)}{x-1}$$

Wie geht es dann weiter?

---

Wie bist Du auf ln(1-x) / (x-1) gekommen?

Answer 2

Hallo julia9105,

.........................................................