Hallo Nico,
mach Dir auf jeden Fall mal eine Zeichnung, so wie diese:
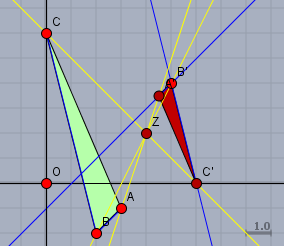
Bei der Konstruktion ist es wichtig zu wissen, dass Geraden durch eine zentrische Streckung in parallele Geraden überführt werden. So bestimmt man den Punkt \(C'\), indem man eine zu \(BC\) Paralle durch \(B'\) zeichnet. Diese schneidet dann die X-Achse in (6|0).
Eine Berechnung geht wie folgt:
$$B'= Z + k \cdot BZ = Z + k \cdot (B - Z)= k \cdot B + (1-k)\cdot Z \quad \Rightarrow (1-k)\cdot Z = B' - k \cdot B$$
Das ganze kann ich jetzt genauso für \(C\) machen und dann den Term \((1-k)\cdot Z\) dort aus der obigen Gleichung ersetzen. Daraus folgt:
$$C' = k \cdot C + B' - k \cdot B = k \cdot (C - B) + B'$$
Schaue ich mir jetzt nur die zweite Koordinate dieser Gleichung an, und setzte die Zahlen ein, so steht dort:
$$ 0 = k \cdot (6 - (-2)) + 4 \quad \Rightarrow k=-\frac{1}{2}$$
Daraus und aus der Gleichung für \(B'\) (s.o.) kannst Du jetzt sofort \(Z\) berechnen - \(Z=(4|2)\). Den Rest schaffst Du alleine - oder?