Wie die Integrationsgrenzen wählen bei Polarkoordinaten r(phi) = 2 - cos(2*phi)?

Question

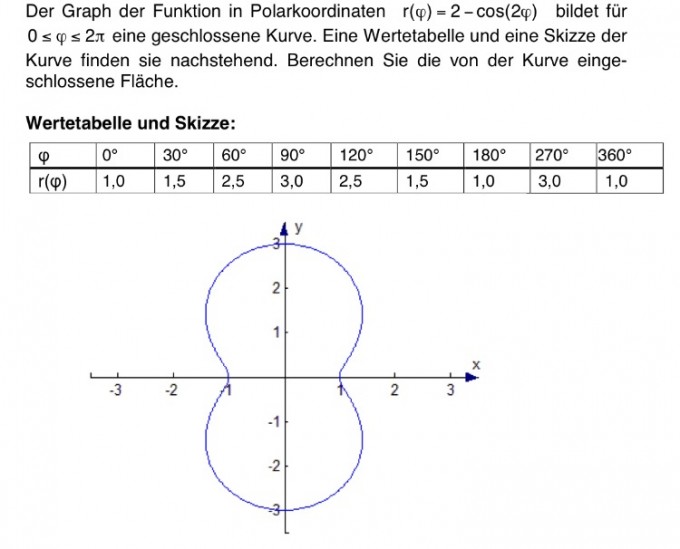
Hab ein Problem beim integrieren von Polarkoordinaten.

Bzw. das integrieren selber ist kein problem, nur das wählen der integralgrenzen verstehe ich nicht wirklich.

Wie muss ich hier die Grenzen wählen um die Fläche zu berechnen?

-1 als untere und 1 als obere Grenze geht wahrscheinlich nicht oder?

danke für die Hilfe

Answer 1

es ist A=∫∫dA

wobei dA=rdrdφ ist. Die Integrationsgrenzen sind nun zu bestimmen.

Der Winkel φ läuft von 0 bis 2π.

Durch r=2-cos(2φ) läuft der Radius von 0 bis 

2-2cos(2φ)

Dabei ist zu beachten, dass man zuerst die r Integration durchführt.

Comments

Kontrollergebnis:

A  =  ₀∫^2π ( ₀∫^2-cos(φ)  r  dr ) dφ  =  9π/2

Answer 2

Warum integrierst du nicht in Polarkoordinaten. Eine Umrechnung auf x-y-Koordinaten erscheint mir hier doch etwas mühsam.

Wenn ich mich nicht vertan habe sollte da etwas in dieser Art stehen.

∫ (0 bis 2·pi) (∫ (0 bis 2 - COS(2·φ)) (r) dr) dφ = 9/2·pi