Mehrdimensionale Integration: fläche Berechnen, Transformation auf Polarkoordinaten, richtige Integrationsgrenzen?

Question

Aufgabe:

Mehrdimensionale Integration: fläche Berechnen, Transformation auf Polarkoordinaten, richtige Integrationsgrenzen?

Problem/Ansatz:

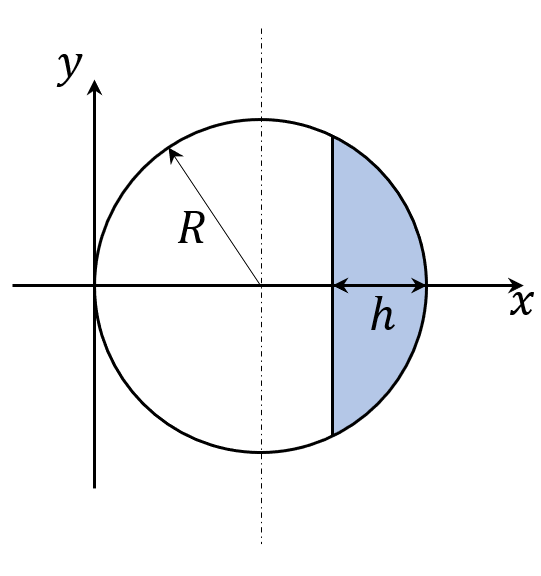
Die Aufgabe ist von mir selbst formuliert.

Ich möchte die blaue Fläche anhand des Parameters \(h\) berechnen.

\(h\in \left[0,\text{ } 2*R\right]\)

Mein Ansatz war mit Hilfe der Transformation auf Polarkoordinaten:

\(2*\int \limits_{\frac{A}{2}}^{}dF \\ =\int \limits_{0}^{arccos(\frac{R - h}{R})}\int \limits_{2*R-h}^{2*R}  r \text{ }drdφ\\= 2*arccos(\frac{R-h}{R})[\frac{1}{2}(2*R)^{2}-\frac{1}{2}(2*R-h)^{2}] \\ = arccos(\frac{R-h}{R})[(2*R)^{2}-(2*R-h)^{2}]\)

Allerdings erscheint mir das Ergebnis nicht plausibel und ich finde den Fehler nicht.

Ich bedanke mich schonmal für Unterstützung!

Comments

Deine Integrationsgrenzen in r - Richtung sind falsch (sie müssen vom aktuellen Winkel abhängen), dadurch berechnest du die blaue Fläche.

---

Sehr gut, danke für den Hinweis!

Wie würden sich hier neue Grenzen gestalten?

Darf ich fragen, welches Tool du für den Plot benutzt hast?

---

welches Tool

GeoGebra.

---

In meiner Skizze habe ich mich von der Tatsache verwirren lassen, dass du offenbar r vom x-y-Koordinatenursprung aus misst, den Winkel φ aber vom Kreismittelpunkt aus.

Answer 1

Ich würde das wie folgt machen

Kreisgleichung

(x - r)^2 + y^2 = r^2 --> y^2 = r^2 - (x - r)^2 = 2·r·x - x^2

Flächenberechnung

A = ∫ (2·r - h bis 2·r) (2·√(2·r·x - x^2)) dx = r^2·ASIN(h/r) + h·√(r^2 - h^2)

Ich habe das jetzt aber nicht großartig geprüft.