Man kann natürlich brute force einfach das nach der Reihe durchrechnen und sehen bis man einen negativen Wert hat:
47000*1.0615-15000 =34890.5
34890.5*1.0615-15000 =22036.265...
22036.265...*1.0615-15000 =8391.496...
8391.496...*1.0615-15000 =-6092.426...
Also bis zum 3ten mal reicht das Geld.
Nun wollen wir das aber etwas allgemeiner machen. Wenn man sich die ersten Jahre ansieht, kommt man schnell hinter ein Schema.
Ko...Startkapital
Kn...Kapital nach n Jahren
A... Zahlung am Ende des Jahres
p... Faktor Prozentsatz (also hier für 6.15% haben wir den Faktor 1.0615)
Betrachten wir nun die ersten paar Jahre:
K1=Ko*p-A
K2=K1*p-A=(Ko-p-A)*p-A=Ko*p^2-A*p-A
K3=K2*p-A=Ko*p^3-A*p^2-A*p-A
... usw.
Insgesamt für Kn Jahre also die Formel
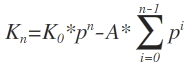
indem wir die Identität
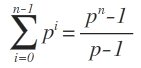
für die Summe verwenden (Nachzulesen z.B.: https://de.wikipedia.org/wiki/Geometrische_Reihe), können wir folgendermaßen vorgehen:
Wir wollen K_n = 0 und es folgt mit oben genannter Identität:
K_0*p^n=A*(p^n-1)/(p-1) =A*(p^n/(p^n*(p-1))-1/(p^n*(p-1)))=A*(1/(p-1)-1/(p^n*(p-1)))
elementare Umformungen führen nun auf:
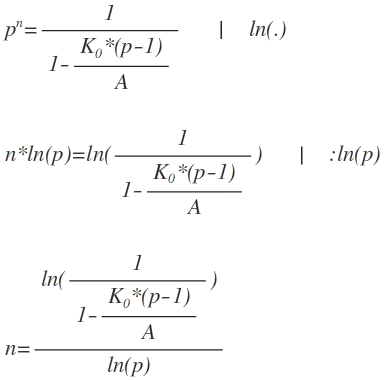
[Der ln sollte über den ganzen Zähler des Bruches gehen]
Einsetzen unserer Werte Ko=47000, p=1.0615, A=15000
liefert für n einen Wert von 3.5866...
Also es bestätigt sich, was wir oben bereits stur durchgerechnet haben. Das beim 4ten Mal das Geld nicht mehr reicht.