cos(5pi/8) bestimmen mit Halbwinkelformel

Question

ich soll cos (5pi/8) bestimmen. Dazu soll ich die Halbwinkelformel benutzen, die folgendermaßen lautet:

cos (θ/2) = √(((1+cos(θ))/2)

Das heißt also:

cos ( (1/2) * (5pi/4)) = √(((1+cos(5pi/4))/2)= √(((1-((√2)/2))/2)= √((2-√2)/2)

Passt das so?

Answer 1

ob das so passt oder nicht, kannst Du leicht selbst mit dem Taschenrechner prüfen - im letzen Term hast Du Dich verrechnet. Da \(\cos{\left( \frac{5}{8}\pi\right)}\) sicher <0 ist, spendiere ich auch noch ein Minuszeichen:

$$\cos{\left( \frac{1}{2} \cdot \frac{5}{4}\pi\right)} =- \sqrt{\frac{1 + \cos{\left( \frac{5}{4} \pi\right)}}{2}}= - \sqrt{\frac{1 - \frac{1}{2}\sqrt{2} }{2}}$$

$$\space = - \frac{1}{2} \sqrt{4 \frac{1 - \frac{1}{2}\sqrt{2} }{2} } = - \frac{1}{2} \sqrt{2 - \sqrt{2}} \approx -0,3827$$

Gruß Werner

Comments

Fehlt also hier das Minuszeichen?

https://www.mathway.com/popular-problems/Trigonometry/301063

---

Ja - schaue Dir den Winkel \(\frac{5}{8}\pi\) im Einheitskreis an:

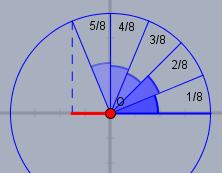
Die rote Strecke ist der Cosinus. Und der zeigt vom Ursprung aus gesehen nach links - ist also negativ. Die Wurzelfunktion liefert lt. Definition immer einen positiven Wert zurück - daher müßte der Halbwinkelsatz eigentlich korrekt heißen:

$$\left| \cos{\left( \frac{x}{2} \right)} \right| =\sqrt{\frac{1 + \cos{\left( x \right)}}{2}}$$

Der Halbwinkelsdatz folgt ja aus dem Additionstheorem

$$\cos(x+y) = \cos(x) \cdot \cos(y) - \sin(x) \cdot \sin(y)$$

$$\Rightarrow \space \cos(x) = \cos^2(\frac{x}{2})  - \sin^2(\frac{x}{2})= \cos^2(\frac{x}{2})  - (1- \cos^2(\frac{x}{2}))$$

$$=2 \cos^2(\frac{x}{2})  - 1$$ $$\Rightarrow \space \cos^2(\frac{x}{2}) = \frac{\cos(x)+1}{2}$$

und beim anschließenden Ziehen der Wurzel, wäre der negative Wert auch eine Lösung dieser Gleichung.