Funktion auf Stetigkeit untersuchen mit 3 Variablen - Frage zum Limes

Question

folgende Aufgabe:

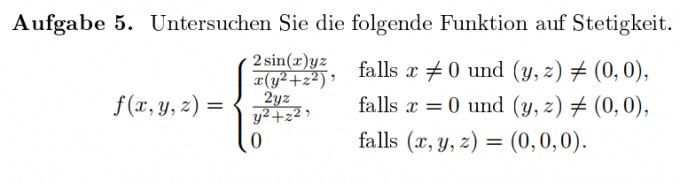
Mein Ansatz:

Für (x,y,z) ungleich (0,0,0) ist die Stetigkeit als Komposition klar.

Zu prüfen: Nähert sich der "erste Teil" dem "zweiten Teil" an, wenn alleine schon x gegen Null läuft. Ich setze also x=1/n und schaue was passiert und sehe: Es kommt Null durch Null raus?! Was tun? Fällt sin(0) einfach weg, wenn ich den Limes dort betrachte?! Nach GWS ja eigentlich nicht...

Für den Übergang von dem Zweiten Teil mit 2yz.... zur Null muss ich einfach (x,y,z) 1/n setzen und n gegen unendlich laufen lassen und dann kommt aber nach kürzen "n" als Ergebnis raus, d.h. die Funktion ist in allen Punkten außer (0,0,0) stetig.

Answer 1

LIM (x --> 0) 2·SIN(x)·y·z/(x·(y^2 + z^2))

= LIM (x --> 0) SIN(x)/x * LIM (x --> 0) 2·y·z/(y^2 + z^2)

= 1 * 2·y·z/(y^2 + z^2)

Der erste und zweite Teil geht also stetig ineinander über.

----------

LIM (y, z --> 0) 2·y·z/(y^2 + z^2)

mit z = m·y

= LIM (y --> 0) 2·y·(m·y)/(y^2 + (m·y)^2)

= LIM (y --> 0) 2·m/(m^2 + 1)

Letzteres ist allerdings von m abhängig und damit ist der zweite und dritte Teil nicht stetig.