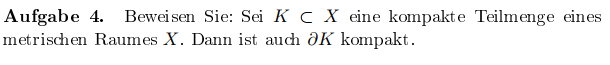Beweise: K aus (M,d) ist kompakt <-> Rand von K ist kompakt

Question

mein Ansatz:
1. Der Rand ist abgeschlossen nach Vorlesung.

2. Aus Abgeschlossenheit folgt: Jede Folge im Rand konvergiert schon auf einen Punkt im Rand

3. Daraus folgt schon direkt Folgenkompaktheit, da jede Folge gegen GW im Rand konvergiert und somit auch jede Teilfolge.

Ist das so korrekt?

Comments

Bei 1. wird in der Regel die Nummer oder Benennung des entsprechenden Satzes in der Vorlesung erwartet.

Answer 1

Ist so wohl OK. Allerdings könnte wohl auch leicht:

M beschränkt ==>  Rand von M beschränkt

über

kompakt <=> beschränkt und abgeschlossen

argumentiert werden.

siehe etwa

http://kulla.me/de/artikel/kompakte_menge_eigenschaften_und_beweise/