Etwas spät, aber für eventuell neugierige Leser.
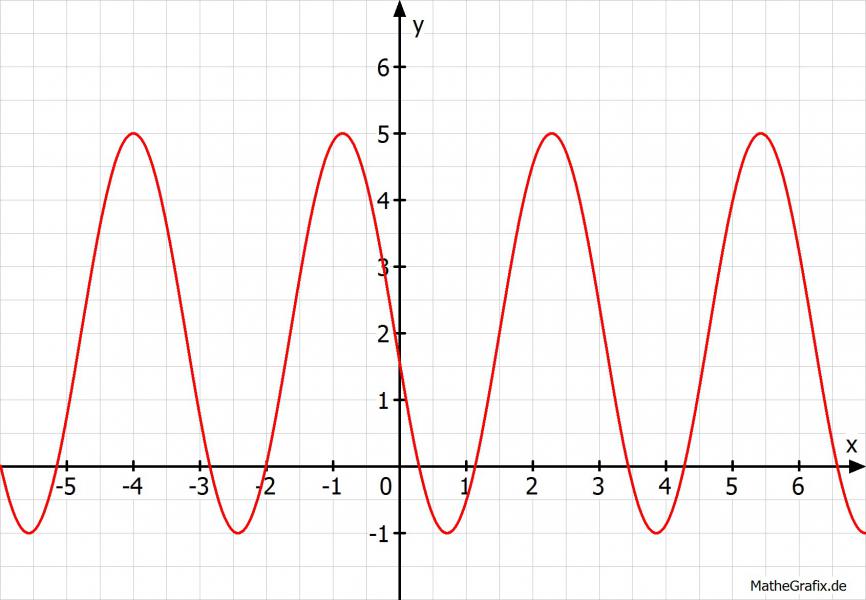
f(x) = 3cos(2x+8)+2
Amplitude: 3
Verschiebung bzgl x-Achse: 2
Periode: π
Nullstellen: f(x) = 0
3cos(2x+8)+2 = 0
3cos(2x+8) = -2
cos(2x+8) = -2/3
x = (±arccos(-2/3)-8)/2
π-Periodizität berücksichtigen!
y-Achsenabschnitt:
f(0) = 3cos(8)+2 = 1,56
Extrema:
f'(x) = -6sin(2x+8)
f''(x) = -12cos(2x+8)
f'(x) = -6sin(2x+8) = 0
x = πn/2 - 4
Wenn man das in die zweite Ableitung setzt erhält man:
Maxima -> x = πn-4
Minima -> x = (2n+1)π/2-4
Wendestellen:
f'''(x) = 24sin(2x+8)
f''(x) = 0
--> x = πn/2 - π/4 - 4
Passt auch mit dritter Ableitung.
Graph:
Grüße