Hallo reeeex,
Die Lösung geht zweimal über den Satz des Pythagoras. Dazu habe ich Dir ein Bild angefügt. (drauf klicken!)
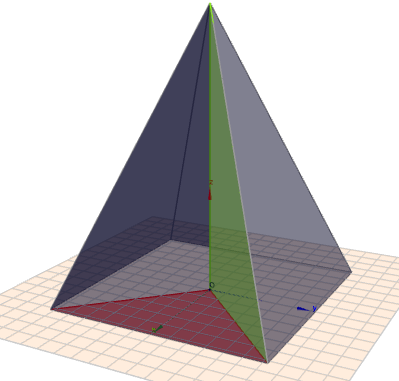
Dort siehst Du ein rötliches Dreieck, das auf dem Boden der Pyramide liegt und ein grünliches Dreieck, was senkrecht innerhalb der Pyramide steht. Der Winkel am Mittelpunkt der Grundfläche ist für beide Dreiecke ein rechter. Ich nenne die Länge einer Diagonal der Grundfläche mal \(d\). Dann besteht das rote Dreieck aus den Seiten \(d/2\), \(d/2\) (die Katheten) und \(a\) (der Hypotenuse) und es gilt nach Pythagoras:
$$\left( \frac{d}{2} \right)^2 + \left( \frac{d}{2} \right)^2 = a^2 \quad \Rightarrow \space \left( \frac{d}{2} \right)^2 = \frac{1}{2}a^2$$
Das grüne Dreieck hat die Seiten \(d/2\), \(h\) (die Kateten) und \(s\) (die Hypotenuse). Und wieder gilt nach Pythagoras
$$\left( \frac{d}{2} \right)^2 + h^2 = s^2$$
Für den Term \((d/2)^2\) setze ich das aus der ersten Gleichung ein, und erhalte:
$$s^2=\frac{1}{2}a^2 + h^2 = \frac{1}{2} 12,5^2\text{cm}^2 + 15^2 \text{cm}^2 = 303,125 \text{cm}^2 $$
Und daraus folgt dann \(s=\sqrt{303,125 \text{cm}^2} \approx 17,4\text{cm}= 174\text{mm}\).