Wasserspiegel, Graph einer Funktion, Gehalt mit Grundgehalt

Question

Aufgaben (funktionale Zusammenhänge, Funktion und Relationen):

1.1 Ein Schwimmbecken wird mit Wasser gefüllt. In jeder Stunde steigt der Wasserspiegel um 0.4m0.4m. Die Wasserhöhe des gefüllten Beckens beträgt 2.5m2.5m. Stelle die Höhe des Wasserstandes 

a) in einer Wertetabelle,

b) in einem Koordinatensystem dar und

c) nenne die jeweilige Zuordnungsvorschrift == Funktionsgleichung für die Wasserstandhöhe (H)(H) in Abhängigkeit von der vergangenen Zeit (t)(t).

d) Nach wie vielen Stunden ist das Becken gefüllt?

1.2. Die Reno GmbH zahlt Vertretern im Außendienst 2000 € Grundgehalt pro Monat. Zusätzlich erhält jeder eine Provision in Höhe von 5 % seines Monatsumsatzes.

a) in einer Wertetabelle,

b) in einem Koordinatensystem dar und

c) nenne die jeweilige Zuordnungsvorschrift == Funktionsgleichung für die Wasserstandhöhe (H)(H) in Abhängigkeit von der vergangenen Zeit (t)(t).

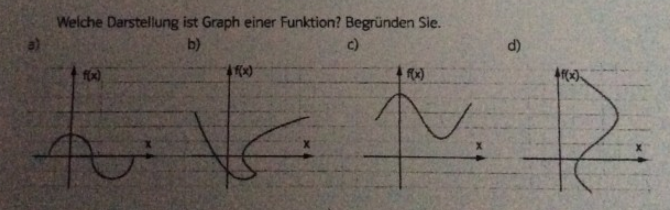
2. Welche Darstellung ist Graph einer Funktion? Begründen Sie.

Comments

EDIT: Habe gerade eine Begriffsrecherche gestartet zu Wasserstand, Pegelstand und Wasserspiegel, da ich mir unsicher war, ob Pegel und Spiegel eigentlich dasselbe Wort ist. Wohl eher nicht. Falls das jemand anders noch interessiert:

https://de.wiktionary.org/wiki/Wasserstand 

https://de.wiktionary.org/wiki/Wasserspiegel

https://de.wiktionary.org/wiki/Pegel 

Answer 1

2. a) und c) sind Graphen von Funktionen. Begründung: Sie ordnen in einem Definitionsbereich, den du so breit zu machen hast, wie die Kurve, die du siehst,  jedem x einen Wert f(x) zu.

Bei b) und d) findet man x-Werte, denen zwei Werte f(x) zugeordnet werden müssten. Das ist bei Funktionen nicht erlaubt. Mehr dazu hier https://de.wikipedia.org/wiki/Funktion_(Mathematik)#Definition

Answer 2

1.1.

Hallo Whege,

die Wertepaare kannst du der Tabelle entnehmen. Die Geradengleichung daraus lautet

f(x) = 0,4x

Um die Zeit bestimmen zu können, nach der das Becken gefüllt ist, setzt du für f(x) 2,5 ein. Daraus ergibt sich x = 6,25, also sechs Stunden und fünfzehn Minuten.

Comments

 Dank für den Rechnungsschritt, leider verstehe ich die Wertetabelle nicht ganz

---

leider verstehe ich die Wertetabelle nicht ganz

Nach einer Stunde beträgt der Wasserspiegel 0,4 Meter. Nach zwei Stunden sind es 0,8 Meter, nach drei Stunden 1,2 Meter, usw.