Graph der Ableitungsfunktion f' der Funktion f. Warum ist diese Aussage nur teilweise richtig/falsch?

Question

ich verstehe die Lösung für die D nicht: 

Fig. 1 zeigt den Graphen der Ableitungsfunktion f' einer Funktion f. Welche der folgenden Aussagen sind wahr? Begründen Sie ihre Antworten. D) Für alle x im Intervall [-2;0] gilt f(x) > 0. 

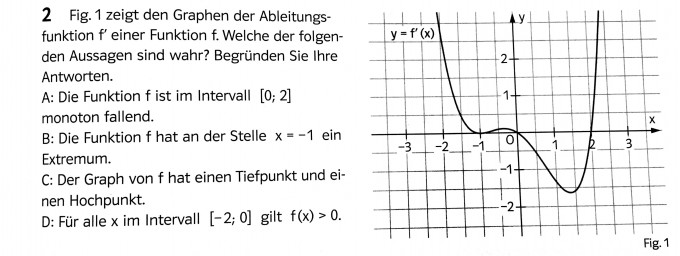
Lösung: Das kann man nicht ohne weiteres entscheiden. Zwar ist f in [-2;0] monoton wachsend, da fort f'(x) ≥ 0 gilt. Wenn f(-2) kleiner oder gleich 0 ist, ist die Aussage D falsch. Wenn f(-2) größer als 0 ist, ist die Aussage D richtig.

Was hat das ganze den mit f(-2) zu tun? Der Graph im Intervall [-2;0] ist doch in f'(x) die ganze Zeit im positiven Bereich bzw. 0..

Answer 1

im Bereich [-2,0] ist die Ableitung f'(x)>=0,

daher die Funktion verläuft monoton wachsend. Es gibt allerdings unendlich viele Funktionen f(x) welche die Ableitung f'(x) besitzen, sie unterscheiden sich alle durch eine additive Konstante (die beim ableiten dann wegfällt). Man kann diese Konstante so wählen, dass f(-2)<0.

Dann ist aber die Behauptung d) auch schon widerlegt.

Answer 2

f ´( x ) ist die Funktion der Steigung einer Funktion.

Wo sich im Koordinatensystem die Funktion f ( x )
befindet kann aus f ´( x ) generell nicht
geschlossen werden.

Ich schreibe es einmal so
f ( x ) = ∫ f´( x ) dx + c

c ist die Integrationskonstante und zunächst
noch nicht bekannt.