Graphen zeichnen zur Funktion f(x)=3x³-5x-3. Nullstellenbestimmung

Question

Kann mir jemand den Graphen zeichnen und erklären wie ich sowas in Zukunft leicht hinbekommen kann und woher ich weiß wieso das so ist.


Zusatz:

f(x)= 3x³ - 5x- 3

a) wie berechnet man die nullstellen.

b) Integral in (-2/1)

Ich vertehe nicht wie das geht  Und erklären was ein Integral nochmal ist.

Comments

Hi,

hier ist iwas merkwürdig.

f(x)=3x³-5x=3

Du meinst f(x)=3x³-5x-3 ?

---

Unsere Lehrerin hat uns das so geben wie ich das schon geschrieben habe. Was ist denn daran falsch?

---

Eine Funktion kann nicht beschrieben werden durch x^3-5x und gleichzeitig durch 3. Ganz sicher, dass das letzte Zeichen nicht ein Minuszeichen sein soll?

Eventuell hast Du unsauber abgeschrieben ;).

---

Geht das denn auf wenn das = ein minus Zeichen wäre? Wenn ja würdest du meine beiden fragen beantworten? Also Nullstellen, Integral in (-2;1) und den Graphen. Kannst du beides hier machen.

---

Ich sperre mal die Aufgabe drüben und mache beides hier.

Die Funktion ändere ich außerdem zu f(x)=3x³-5x-3.

Einverstanden? ;)

---

ja und wie. du bist meine rettung :) wie lange brauchst du?

---

Kennst Du das "Newtonverfahren"? Die Nullstelle ist nämlich "krumm" und nicht so leicht zu bestimmen.

---

Ne kenne ich nicht aber was neues ist immer gut. Wenn du mir es in der rechnung gut erklärst verstehe ich es bestimmt und wenn nicht kann ich dich ja immer nochmal fragen. Also benutze es ruhig.

---

Dann eine letzte Frage :P.


-> Integral in (-2/1)

Sehr unüblich das Integral an einem Punkt zu erfragen. Du meinst etwa die Ableitung?

Abgesehen davon, liegt (-2|1) gar nicht auf dem Graphen.

Oder ist das Intervall von -2 bis 1 gemeint? Also [-2,1]

---

Das ist in der Tat merkwürdig! Ich werde das morgen nochmal fragen. Also kannst du ruhig weglassen. Unsere Lehrerin ist etwas merkwürdig O-O. Also brauche ich nur noch den Graphen und die Nullstellen bitte.

Sag mal bist du Lehrkraft für Mathe oder einfach jemand der Mathe in gegensatz zu mir versteht?

Answer 1

Sodelle,

nachdem einiges geklärt wurde.

Zeichnen:

f(x)= 3x³ - 5x- 3

Um das zu zeichnen, mache eine Wertetabelle. D.h. Du nimmst Dir verschiedene x-Werte (x=-3...x=3).

Bestimme die zugehörigen y-Werte und trage in das Schaubild ein.

Du solltest dann auf etwas in dieser Gestalt kommen (man sieht schon, wie "blöd" diese Funktion ist^^)

 

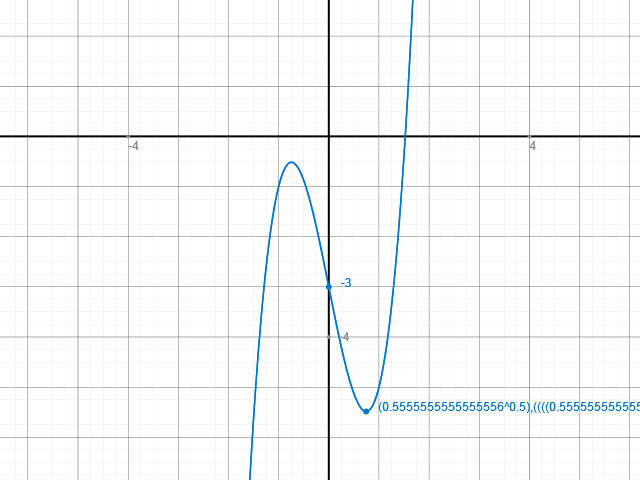
Du siehst ebenfalls schon eine Nullstelle, die zwischen 1 und 2 liegt. Da hilft nun das Newtonverfahren.

Das Newtonverfahren hat die Formel:

$$x_{i+1} = x_i-\frac{f(x_i)}{f'(x_i)}$$

wobei x₀ = 1,5 ist. Die 1,5 sind frei gewählt, aber wir vermuten ja die Nullstelle in dieser Nähe

f'(x) = 9x²-5

 

Los gehts:

$$x_{0+1} = x_1 = 1,5-\frac{3*(1,5)^3-5*1,5-3}{9*(1,5)^2-5} = 1,5246$$

Um x₂ zu berechnen, gehe genauso vor. Allerdings ist x₁ ja 1,5246 und nicht mehr 1,5 ;).

Ich habe:

x₂ = 1,5241

x₃ = 1,5241

 

Damit kann man eigentlich schon aufhören. Wie wo und warum das so ist, ist auf die Schnelle natürlich etwas schwer erklärt und ich würde es für den Anfang mal hinnehmen. Wenn Du genauers am Newtonverfahren interessiert bist, schau mal im Schulbuch nach  ;).

 

Die Nullstelle ist also x = 1,5241

 

Alles klar?

Grüße

Comments

ja alles klar. danke. Du bist einfach genial.

---

Danke :). Es freut mich, wenn ich helfen konnte ;).