Gegeben sind die Geraden f(x)=3x-8 und g(x)= 3x+2
Begründe, dass f und g paralell zueinander sind
Beide Funktionen haben dieselbe Steigung,
verlaufen also bis in alle Ewigkeit parallel
zueinander.
Berechne den Abstand der beiden Geraden
Kann bitte jemand helfen?
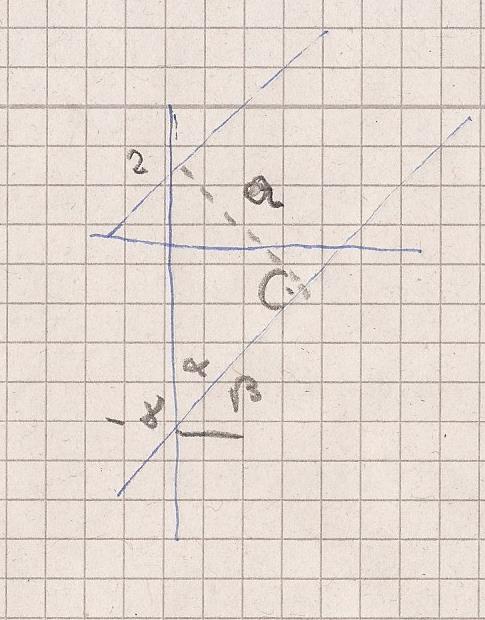
Steigung = 3
Winkel beta = arctan ( 3 ) = 71.565 °
Winkel alpha = 90 - 71.565 = 18.435 °
Die beiden Funktionen schneiden die y-Achse
bei 2 und -8 und sind dort 10 Einheiten auseinander
a ist der Abstand ( lotrecht zu beiden Funktionen )
sin ( alpha ) = a / 10
sin ( 18.435 ) = a / 10
a = 3.162
Der Abstand beträgt 3.162
Alle Angaben ohne Gewähr.