Hallo JF,
in den Sonderfällen Q=B (P=M) und Q=C (P=C) trfft die Behauptung - im ersten Fall offensichtlich, im zweiten Fall nach Pythagoras - zu. Es wäre deshalb eher überraschend, wenn das "zwischendurch" anders wäre :-) :
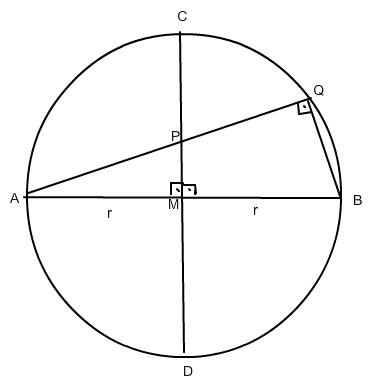
Thalessatz → ΔABQ ist rechtwinklig. (für Q≠B,C)
Die Dreiecke ABQ und AMP sind also ähnlich (zwei gleiche Winkel).
Entsprechende Seiten (maßgleichen Winkeln gegenüberliegend) stehen also im gleichen Verhältnis.
→ r / AP = AQ / (2r) | * AP | * 2r
→ 2 * r^2 = AP * AQ
Gruß Wolfgang