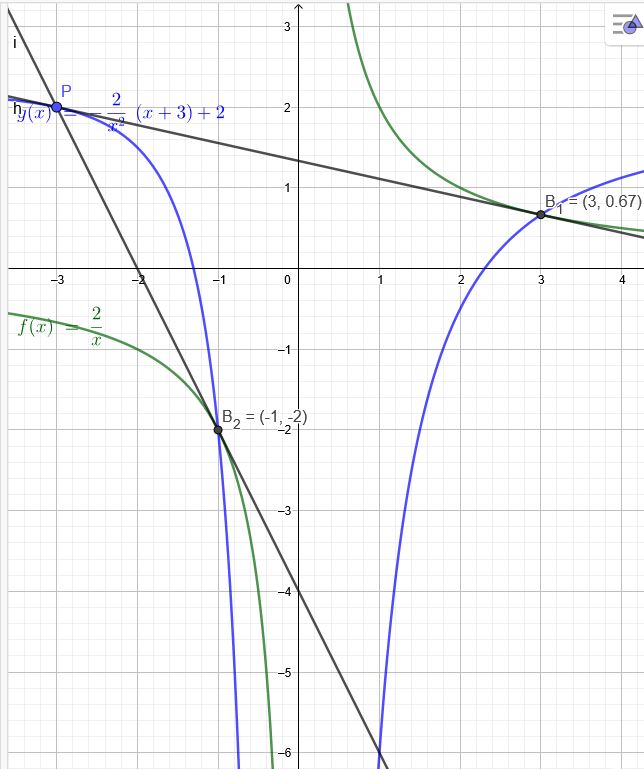
\(f(x)=\frac{2}{x}\) Tangentengleichungen durch den Punkt \(P(-3|2)\) :
Berührpunkte haben die Koordinaten \(B(x|\frac{2}{x})\) \(f´(x)=-\frac{2}{x^2}\)
\( \frac{\frac{2}{x}-2}{x+3}=-\frac{2}{x^2} \) mit \( x≠ 0\) und \(x≠-3 \)
\( \frac{2-\frac{2}{x}}{x+3}=\frac{2}{x^2} \)
\( 2x^2-2x=2x+6 \)
\( 2x^2-4x=6 \)
\( x^2-2x=3 \)
\( (x-1)^2=3+1=4 \)
1.)
\( x-1=2 \)
\( x_1=3 \) \(f(3)=\frac{2}{3}\) \(f´(3)=-\frac{2}{9}\)
2.)
\( x-1=-2 \)
\( x_2=-1 \) \(f(-1)=-2\) \(f´(-1)=-2\)
Nun noch die Tangentengleichungen aufstellen.
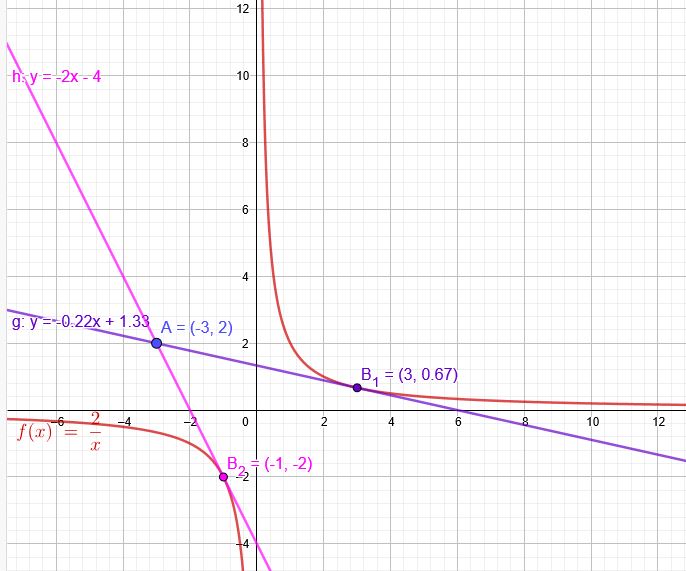
2.Weg:
\(f(x)=\frac{2}{x}\) \(f'(x)=-\frac{2}{x^2}\)
\(P(-3|2)\):
\( \frac{y-2}{x+3}=-\frac{2}{x^2} \)
\( y=-\frac{2}{x^2}(x+3)+2 \)
Schnitt mit \(f(x)=\frac{2}{x}\) gibt die x-Werte des Berührpunktes:
\( -\frac{2}{x^2}(x+3)+2=\frac{2}{x} |\cdot x^2 \)
\(2\cdot x^2-4x =6 \)
\( x^2-2x =3 \)
\( (x-1)^2 =4 |±\sqrt{~~}\)
\(x_1=3\) \(f(3)=\frac{2}{3}\)
\(x_2=-1\) \(f(-1)=-2\)
Nun noch die Tangenten ausrechnen.