Wie weit hängt das Bild tiefer als die beiden Nägel? Wie groß sind die Winkel α und β? (Vektoren)

Question

HM Aufgabe - Vektoren 2, Lineare Gleichungssysteme:

1. Zwischen zwei Nägeln, die in gleicher Höhe im Abstand von \( 1,5 \mathrm{~m} \) in der Wand stecken, hängt an einem \( 1,8 \mathrm{~m} \) langen Seil ein Bild mit einem wertvollen, schweren Rahmen. Das Seilstück vom Bild zum linken Nagel ist \( 50 \mathrm{~cm} \) lang, zum rechten Nagel \( 1,3 \mathrm{~m} \). Das Bild hat eine Masse von \( 12 \mathrm{~kg} \).

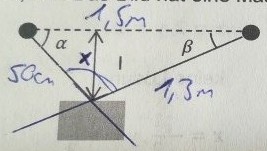
a) Wie weit hängt das Bild tiefer als die beiden Nägel?

b) Wie groß sind die Winkel \( \alpha \) und \( \beta \) ?

c) Mit welcher Kraft zieht das Bild jeweils am linken und am rechten Nagel? Anleitung: Die Gewichtskraft des Bildes wird auf die beiden Seilstücke verteilt. Die Summe der beiden Kräfte weist senkrecht nach oben.

Answer 1

Mit Pythagoras gewinnst du zwei Gleichungen:x²+y²=50² und x²+(150-y)²=130². Zwei Gleichungen mit zwei Unbekanntenkannst du lösen, oder?

Comments

Im Prinzip schon aber irgendwie bekomm ich ein falsches Ergebnis wäre echt nett wenn du mir kurz den Rechenweg zeigen könntest :)

---

Die Gleichungen Subtrahieren ergibt: y²-(22500-300y+y²)=50²--16900 und dann y=27. Dann ist x≈42,1.