Question

cosα=sin31.8° definitionsbereich 0° bis 90°

ich wäre vor allem über den lösungsweg dankbar, da ich noch weitere aufgaben dieser art lösen soll

zb

sinα=1/3cos210.3°

Comments

sinα=1/3cos210.3°

Du meinst:

sinα=1/3 cos(210.3°) 

und nur die 3 ist unter dem Bruchstrich? 

Rechne 

α= arcsin((1/3)* cos(210.3°) ) =  -16.726°

Hier müsste nun wohl der Definitionsbereich ein anderer sein. In den müsste man noch umrechnen. 

Answer 1

Tipp:

$$ cos(\alpha)=sin(90°-\alpha) $$

Comments

wie kann man das wissen?und welches ergebnis bekommt man schlussendlich?

---

Im rechtwinkligen Dreieck gibt es neben dem rechten Winkel 2 Winkel:

α und β. 

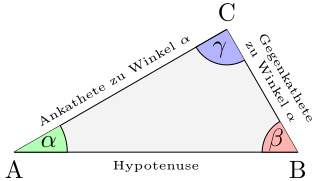
Aufgrund der Innenwinkelsumme von 180° gilt α+β=90°

und damit β=90°-α .Gleichzeitig ist die Ankathete zu α auch die Gegenkathete zu β.

Berechne nun den Cosinus und Sinus mithilfe der Definition und vergleiche.

$$ sin(\beta)=\frac { { Gegenkathete }_{ \beta } }{ Hypotenuse }=\frac { { Ankathete }_{ \alpha } }{ Hypotenuse }\\=cos(\alpha)\\sin(\beta)=sin(90°-\alpha)\\\to cos(\alpha)=sin(90°-\alpha) $$

Berechne nun α mithilfe der Gleichung

$$ 90°-\alpha=31.8° $$

Answer 2

sin 31,8 = 0,52696

cos α = 0,52696

α= 58,2° (TR: drücke: shift cos 0,52686)

Comments

oh wow?! dann habe ich es ja richtig, die lösung im buch gibt aber 58,92°an 

---

und was für einen wert kriegt man für die zweite aufgabe?

---

dann habe ich es ja richtig, die lösung im buch gibt aber 58,92°an 

Du hast das richtig! Kontrolle: Die Summe von alpha und beta muss 90° sein, damit die Winkelsumme im Dreieck (180°) stimmt.