Hängebrücke als quadratische Funktion? Länge der Tragseile? Fläche Werbeverkleidung?

Question

die Aufgabe lautet:

Hängebrücke

Eine Hängebrücke wird von zwei Stahlseilen getragen, die parbelförmig zwischen den Pylonen verlaufen. Acht Tragseile auf jeder Seite tragen die eigentliche Fahrbahn.

a) Stellen Sie das vordere Stahlseil durch eine quadratische Funktion dar.

b) Wie lang sind die acht Tragseile, die am vorderen Stahlseil hängen?

c) Welchen Flächeninhalt haben die vier Werbeverkleidungen zwischen den Tragseilen?

Hierzu eine Skizze:

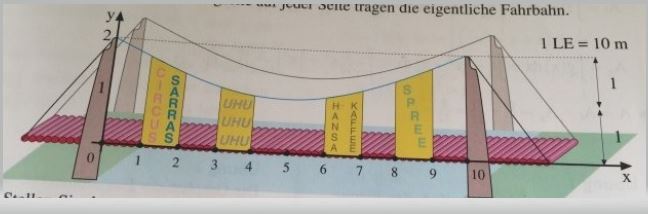
 Wie löse ich diese Aufgabe?

Answer 1

Hallo Guido598! :-)

a)
Scheitelpunktform f(x) = a(x - xs)^2 + ys
Scheitelpunkt abgelesen: (xs | ys) = (5 | 1) und
in f(x) eingesetzt f(x) = a(x - 5)^2 + 1
Fehlt noch das a, wir kennen den Punkt (0 | 2)
2 = a(0 - 5)^2 + 1
Auflösen nach a gibt  a = 1/25 und damit die Funktionsgleichung
f(x) = 1/25(x - 5)^2 + 1

b)
Berechne f(1), f(2), f(3) ... usw.

c)
Integriere von 1 bis 2 und von 2 bis 3.

Beste Grüße
gorgar

Comments

Hast du nicht vielleicht hier und da ein Quadrat Vergessen?

---

Exakt! Hier und sogar auch da! Korrigere es...

---

Hallo Gorgar,
Integriere von 1 bis 2, von 2

besser
Integriere von 1 bis 2, von 3 bis 4

Da die Angelegenheit symmetrisch ist
wiederholen sich die beiden Flächen
nur noch.

---

Uuuuups, da war der Satz abgebrochen, danke! :-)

---

Eine Frage woher kommt denn die 1,2,3 usw. bei f( )....

---

Die Parabel hat die Funktion
f ( x ) = 1/25 * ( x - 5 )^2 + 1 und gibt u.a die Höhe oder
die Länge der Tragseile an

b)
Berechne f(1), f(2), f(3) ... usw.
f ( 1 ) = die Höhe an der Stelle x = 1 m
1,2,3,4 ist symmetrisch zu 6,7,8,9

---

Oh okay und zu c muss man da nicht für 1 bis 2, 3-4, 6-7 und 8-9 integrieren?

---

Integriere von 1..2  und 3 .. 4
Da das Bauwerk symmetrisch ist ist
1..2 gleich 6 .. 7
und
3..4 gleich 8..9
( siehe Skizze )