Funktion 3.Grades aufstellen

Question

ich bräuchte da hilfe bei der Aufgabe 1.1 , 1.2 und 1.3

Answer 1

f (0)= 0

f '(0) =0

f(6)= 0

f '(6)= 9

Comments

f'(6) = 9\(\).

---

Danke, habs verbessert. :)

Answer 2

f ( 0 ) = 0
f ' ( 0 ) = 0
f ( 6 ) = 0
f ' ( 6 ) = 9

Falls dir die Kurzschreibweise der Aussagen
nicht geläufig ist dann bitte nachfragen
ebenso
wenn du noch weitere Hilfe benötigst.

Zur Kontrolle
f(x) = 0,25·x^3 - 1,5·x^2

Comments

g ( x ) = 1/4 * x^3 - 3/2 * x^2

Tiefpunkt berechnen
g ´( x ) = 3 / 4 * x^2 - 6 / 2 * x

3 / 4 * x^2 - 3 * x = 0
x * ( 3/ 4* x - 3 ) = 0
Satz vom Nullprodukt
x = 0
und
3/ 4* x - 3 = 0
x = 3 * 4 / 3
x = 4

Hoch- oder Tiefpunkt
g ´´ ( x ) = 6 / 4 * x - 3
g ´´ ( 4 ) = 6 / 4 * 4 - 3 = 3 ( Tiefpunkt )
g ( 4 ) =  1/4 * 4^3 - 3/2 * 4^2 =
g ( 4 ) = 16 - 24
T ( 4 | - 8 )

h ( x ) = 1/4 * x^3 - 3/2 * x^2 + 8
h ( 4 ) = -8 + 8 = 0
h ( x ) = 1/4 * ( x + 4 )^3 - 3/2 * ( x + 4 ) + 8

---

Für welche x ∈ ℝ gilt
x = 0
und
3/ 4* x - 3 = 0 ?

Answer 3

Hallo Lolo,

1.1

f(x) = ax³ +bx² + cx + d

^{f '(x)  =  3ax^2 + 2bx + c}

^{f(0) = 0   →   d = 0}

^{f '(0) = 0  →  c = 0}

^{f(6) = 0   →}     216·a + 36·b = 0

f '(6) = 9   →   108·a + 12·b = 9

       G1 - 2*G2:    12b = - 18   →   b = - 1,5  = -3/2  

          a  einsetzen  →   a = 0,25 = 1/4

f(x) =  1/4 · x³ - 3/2 · x²

------------

1.2

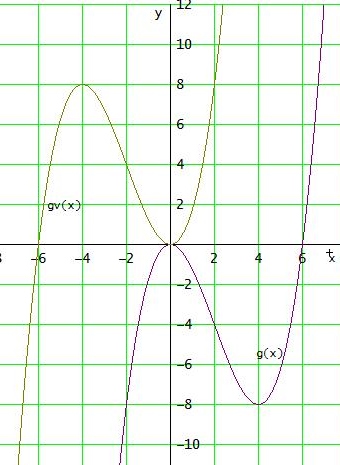
g(x) = 1/4 · x³ - 3/2 · x²   

f '(x) = 3/4 ·x^2 - 3·x  = 0   →     x = 0  oder  x = 4   (Minimumstelle , VZW f ' von - nach +)

 T( 4 | -8)   →  (0|0) 

g muss also um 4 Einheiten nach links und um 8 Einheiten nach oben verschoben werden:

g_v (x) = 1/4 · (x+4)³ - 3/2 · (x+4)²  + 8   =  1/4 · x^3 + 3/2 · x^2

Gruß Wolfgang

Comments

erstmal vielen dank für die Ausführliche Antwort *_*

wenn ich das richtig verstehe, ist d=0 da der Grad die x-Achse im Ursprung berührt. Daher f(0)=0 --> d=0 und die 1Ableitung von der erste Nullstelle gibt Auskunft über c also f'(0)=0 --> c=0

Ich verstehe leider nicht warum hier das rauskommt

f(6)  ^→     216·a + 36·b = 0

und nicht 216*a+36*b+6=0 (wegen dem c*x)

wir setzen ja die 6 in die f(x)= ax^3+bx^2+cx+d oder nicht?

---

> ... wir setzen ja die 6 in die  f(x)= ax³ + bx² + cx + d  oder nicht? 

mit  c = 0 und d = 0  ergibt sich bereits

f(x) =  a·x³ + b·x²

wenn du da  x=6 einsetzt, erhältst du

f(6) = 216·a + 36·b

---

oh ja stimmt da habe ich nicht genau aufgepasst. Vielen lieben dank