Question

Wie bestimme ich ein globales Minimum, Maximum...?

Wenn ich die lokalen Extrempunkte kenne und die Randpunkte, wie mache ich jetzt weiter?

Comments

probe, die bisherigen Antworten leiden stark unter begrifflichen Ungenauigkeiten. Vergiss sie!

Answer 1

Welches aller lokalen Maxima und den Randmaxima ist global der Höchste Wert? Das ist dein globales Maximum.

Welches aller lokalen Minima und den Randminima ist global der niedrigste Wert? Das ist dein globales Minimum.

Comments

Auch Randextrema sind lokale Extrema.

---

Ja. Auch ein Randextrema ist eigentlich ein lokales Extrema.

Es wird aber häufig unterschieden. Wenn man sagt das die notwendige Bedingung für ein lokales Maxima ist, dass die erste Ableitung null wird, dann wird ja eigentlich klar, dass dies für Randextrema nicht notwendig ist.

Dann wäre eigentlich die Bedingung so falsch oder nicht?

---

f(-2pi/3)=e^3/4

Maximum: f(-pi/2)=e

Minimum: f(0)=1

Maximum: f(pi/2)=e

f(2pi/3)=e^3/4

Wie gehe ich jetzt genau vor?

---

Da e^{3/4} = 2.117

Das globale Minimum von 1 wird an der Stelle 0 angenommen.

Das globale Maximum von e wird an den Stellen -pi/2 und +pi/2 angenommen.

(Nachträglich korrigiert)

---

"Ein globales Maximum gibt es nicht, weil der höchste Wert an zwei Stellen angenommen wird."

Das ist nicht richtig, im Beispiel wäre y=e das globale Maximum. Es muss mndestens einmal, kann aber auch auch mehrmals, angenommen werden. y=sin(x) hat beispielsweise die globalen Extrema \(-1\) und \(1\).

---

Oh. Danke für die Korrektur.

Wie ist das genau mit der notwendigen Bedingung für ein lokales Extremum? Wie sollte man das den Schülern am besten auch im Hinblick mit Randextrema vermitteln?

---

Mir ist das irgendwie immer noch nicht ganz klar.

---

Was ist dir nicht klar?

---

ab 10:15 Sind Randmaxima auch lokale Maxima ?

---

"Wie ist das genau mit der notwendigen Bedingung für ein lokales Extremum? Wie sollte man das den Schülern am besten auch im Hinblick mit Randextrema vermitteln?"

Gute Frage! Da es sich um lokale Eigenschaften handelt, wird man wohl auf Epsilon-Umgebungen zurückgreifen und muss die Definitionen dann so formulieren, dass alle Spezialfälle wie Randextrema, nicht differenzierbare Funktionen u.v.a. mit abgedeckt werden. So ähnlich haben wir es im Mathematikunterricht gemacht, allerdings war der Lehrer auch viel detailversessener, als das heuter leider der Fall ist, und wir konnten die exakten Definitionen auch für allerlei Beweise nutzen.

Will man das nicht, etwa weil man dafür gar keine Zeit hat, könnte man eine anschauliche Begriffseinführung über die offensichtlichen Eigenschaften von gezeichneten Funktionsgraphen versuchen. Das sollte natürlich nicht im Widerspruch zu sinnvollen Definitionen stehen.

Answer 2

vergleiche ob die Randpunkte größer/ kleiner als die lokalen Maxima/Minima sind.

Wenn ja, dann ist der Randpunkt globales Maximum/Minimum.

Wenn nein, dann ist einer der lokalen Maxima/Minima das globale Maximum/Minimum.

Comments

Ein Extrempunkt ist kein Extremum und Punkte lassen sich nicht mit Werten vergleichen.

---

Mmh in Deutsch bin ich leider nicht so gut, aber ich dachte es ist im Kontext klar, dass man die y-Werte der Punkte vergleicht.

Answer 3

Hallo Probe,

eine lokale (relative)  Maximumstelle  ist eine Stelle x₁ ∈ D_f , für deren Funktionswert f(x₁) es in einer (genügend kleinen) Umgebung von x₁ keinen größeren anderen Funktionswert gibt. f(x₁) ist dann ein lokales Maximum.

Eine lokale (relative)  Minimumstelle  ist eine Stelle x₂ ∈ D_f , für deren Funktionswert f(x₂) es in einer (genügend kleinen) Umgebung von x₂ keinen kleineren anderen Funktionswert gibt. f(x₂) ist dann ein lokales Minimum.

Eine globale (absulute)  Maximumstelle  ist eine Stelle x₃ ∈ D_f  , für deren Funktionswert es in ganz D_f  keinen größeren Funktionswert gibt. f(x₃) ist dann ein  globales Minimum.

Eine globale (absulute)  Minimumstelle  ist eine Stelle x₄ ∈ D_f  , für deren Funktionswert es in ganz D_f  keinen kleineren Funktionswert gibt. f(x₄) ist dann ein globales Minimum.

Beispiele:

f : ℝ → ℝ :  f(x) = 1/4 · x³ - 2·x² + 4·x

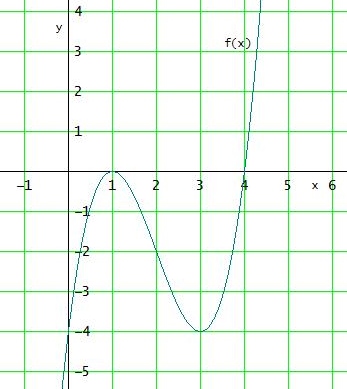
Den Hochpunkt (1|0) und den und Tiefpunkt (3|-4) bestimmen wir wie immer.

Die Monotonieintervalle entnehmen wir ohne weitere Erwähnung einfach dem Graph.

x₁ = 1 ist lokale  Maximumstelle mit f(1) = 0,  denn in  [ 0,5 ; 1,5 ] gibt es keinen größeren Funktionswert

x₂ = 3 ist lokale  Minimumstelle mit f(3) = -4, denn in  [ 2,5 ; 3,5 ] gibt es keinen größeren Funktionswert

Wegen lim_{x → ∞} f(x)  =  ∞  gibt es kein globales Maximum , weil es beliebig große Funktionswerte gibt.

Wegen lim_{x → -∞} f(x)  =  - ∞  gibt es kein globales Minimum , weil es beliebig kleine Funktionswerte gibt.

-------

Ändert man aber für den gleichen Funktionsterm den Definitionsbereich, dann sieht das anders aus:

f : [ 0,5 ; 5 ]  → ℝ :  f(x) = 1/4 · x³ - 2 · x² + 4·x  :

Die beiden lokalen Extremstellen bleiben.

Auch x₃ = 0,5 mit f(0,5) =  - 0.875 ist  jetzt wegen  -4  < f(5) < 0  eine lokale Minimumstelle 

         x₄ = 5  mit f(5) = 16  ist wegen  0 < 16 eine globale Maximumstelle  

                              (und damit natürlich auch lokale Maximumstelle)

Gruß Wolfgang

Comments

Vielen vielen Dank.

:)

---

für dich doch immer :-)