Hallo ani,
Die gemeinsame Fläche - hier \(PXQX'\) - ist eine Raute.
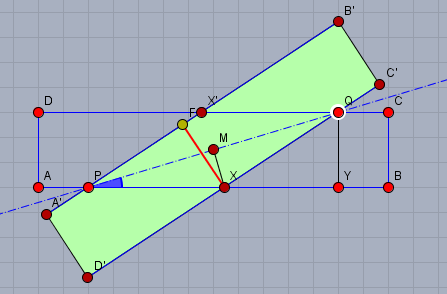
Es reicht also aus, die Strecke \(PX\) zu bestimmen, dann ist die Fläche
$$F=AD \cdot PX$$ Am einfachsten lässt sich \(PX\) wohl über die beiden ähnlichen Dreiecke \(PYQ\) und \(PXM\) bestimmen. \(Y\) ist der Fußpunkt vom Lot des Punktes \(Q\) auf \(AB\) und \(M\) ist der Mittelpunkt der Strecke \(PQ\). Aus der Ähnlichkeit folgt direkt
$$\frac{PX}{PM} = \frac{PQ}{PY}$$
mit \(PM= \frac12 PQ\) also
$$PX = \frac{\frac12 PQ^2}{PY}= \frac{\frac12 \cdot(3^2 + 10^2)}{10}=\frac{109}{20}=5,45$$
und die Fläche ist dann \(F=AD \cdot PX=3\text{cm} \cdot 5,45\text{cm}=16,35 \text{cm}^2\)
Da Du aber in der Überschrift das Wort 'Trigonometrie' stehen hast, hier nach ein zweites Verfahren: Der Winkel \(QPB=\alpha\) (der blaue Winkel) ist
$$\tan( \alpha ) = \frac{QY}{PY}=\frac{3}{10} \quad \Rightarrow \alpha=\arctan(\frac{3}{10}) \approx 16,70°$$ Die Strecke \(XF\) (rote Strecke) ist wieder die Höhe des Rechtecks. Aus dem rechtwinkligen Dreieck \(PXF\) kann man ablesen:
$$\sin(2\alpha) = \frac{XF}{PX} \quad \Rightarrow PX=\frac{XF}{\sin(2\alpha)}\approx\frac{3}{\sin(33,4°)} \approx 5,45$$
Die Lösung ist natürlich die gleiche.
Gruß Werner