Rechteck -> Quadratische Funktion

Question

Die Diagonale eines rechtecks ist 20 cm lang. Die Seitenlänge unterscheiden sich um 8cm. Bestimme die Seitenlänge. 

P.s. Bitte verständlich lösen. Danke ! 

Comments

Tipp: Satz des Pythagoras

Answer 1

x^2+y^2= d^2

x-y=8 --> x=8+y

(8+y)^2+y^2= 20^2

64+16y+y^2+y^2=400

2y^2+16y-336=0

y^2+8y-168= 0

pq-Formel:

y1/2= -4±√(16+168)

y1=

y2=

Die negative Lösung entfällt.

Answer 2

Pythagoras

a^2+b^2=d^2

Ausserdem 

a=b+8

Einsetzen in oben

(b+8)^2+b^2=400

b^2+16b+64+b^2-400=0  | /2

b^2+8b-168=0

Pq-formel 

b_(1,2)=-4±√(16+168)

b=-4+13,56=9,56

a=17,56

Die Werte sind gerundet.

Answer 3

Hallo JB,

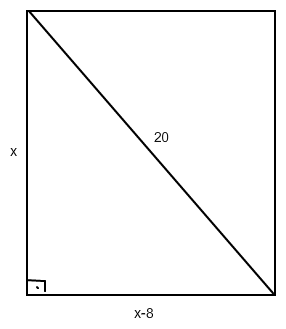
Pythagoras:

x² + (x - 8)² = 20²

x² + x² - 16x + 64 = 400  | - 400

2x² - 16x  - 336  =  0    | :2

x² - 8x -168  = 0

x² + px + q = 0

pq-Formel:  p = - 8 ; q = - 168

x_1,2 = - p/2 ± \(\sqrt{(p/2)^2 - q}\)

....

  x₁ = 2·√46 + 4  ;   x₂  = 4 - 2·√46 

x  ≈   17.56    [  x₂ ≈ - 9.56  entfallt ]

Die große Seitenlänge beträgt  ≈  17.56 cm  ,  die kleine  9.56 cm  

Gruß Wolfgang