gemeinsamen Punkt von Parabel und tangente bestimmen (tangential)

Question

wie könnte ich bei der Aufgabe 7 vorgehen? Bitte gebt mir keine Antworten, sondern nur die Schritte, die ich bestreiten müsste, um diese Aufgabe zu lösen! ;) 

:) 

Answer 1

Du brauchst also eine Tangente mit dem y-Achsenabschnitt 6.

Tangente im Punkt (x;y) hat die Steigung f ' (x) = -x 

und geht durch den Punkt (x ; 4 - 0,5x²  )  . Setze das alles in die 

Tangentengleichung y = m*x + n also y = m*x+6 ein.

Dann kannst du das x ausrechnen. Es gibt sogar 2 davon,

aber eins ist unsinnig.

Comments

Alles klar. Das habe ich gemacht.

4-0,5x^2=-x*x+6

20 + x^2 + 0 = y

Nach pq Formel kommt für x = 4,47 raus. Ist das korrekt?

---

Ich bekomme:

y = m*x + 6

4 -0,5 x² = -x * x + 6

       0,5 x² =  2

x² = 4 

x = 2 oder x=-2 

Nach dem Bild macht nur -2 Sinn.

---

Ist -x*x nicht gleich x^2?

Answer 2

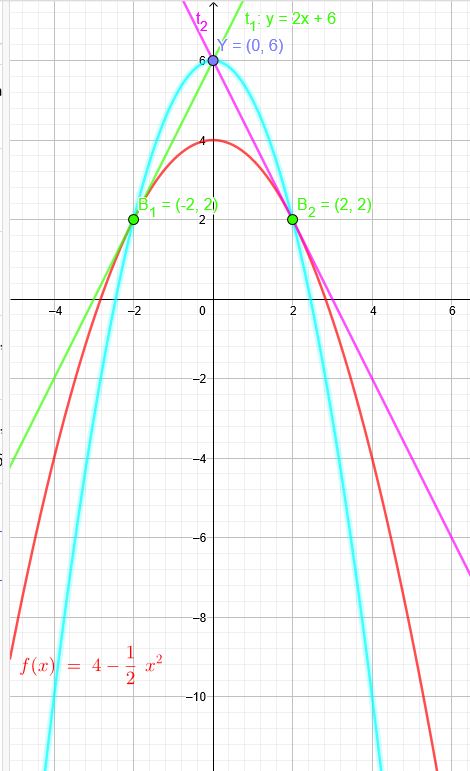
\(f(x)=4-0,5x^2\)   Büschelpunkt    \(Y(0|6)\)

Geradenbüschel durch  \(Y(0|\red{6})\):

\( \frac{y-\red{6}}{x}=m \)

\( y=mx+6 \)

Gleichsetzung Geradenbüschel und Parabel:

\(mx+6=4-0,5x^2 \)

\(0,5x^2+mx=-2 |\cdot 2\)

\(x^2+2mx=-4 \)

\((x+m)^2=-4+m^2   |±\sqrt{~~} \)

\(x+m=±\sqrt{-4+m^2 } \)

Diskriminante =0 ergibt die Steigungen   \(m_1=2\)    \(m_2=-2\)

Berührpunkte bei \(B_1(-2|2)\)  und \(B_2(2|2)\)

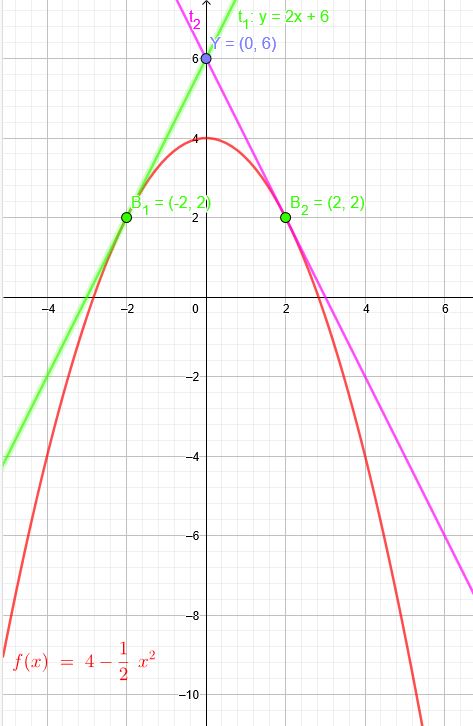
Ein anderer Weg:

\(f(x)=4-0,5x^2\)  Büschelpunkt   \(Y(0|6)\)

\(f'(x)=-x\)

\( \frac{y-6}{x}=-x \)   \( p(x)=-x^2+6 \)  

Diese Parabel schneidet nun \(f(x)\) in den beiden Berührpunkten.

\(-x^2+6 =4-0,5x^2\) 

\(-0,5x^2=-2\)

\(x^2=4 \)  usw