Aufgabe:
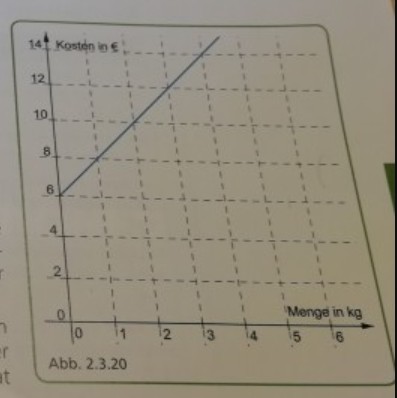
Der Frühling - die Spargelzeit. Im Supermarkt kosten \( 500 \mathrm{~g} \) Spargel regulär \( 2,99 € \). Wenn Sie mit der Bahn zum Bauern aufs Land fahren, so lassen sich die Kosten pro Kilogramm durch die angegebene Grafik darstellen.
a) Stellen Sie für beide Kaufvarianten \( \left(K_{s}\right. \) und \( \left.K_{B}\right) \) eine Funktionsgleichung auf.
b) Ermitteln Sie die Gesamtkosten für \( 4 \mathrm{~kg} \) Spargel am Land bzw. im Supermarkt.
c) Auf einem Bauermarkt lassen sich die Kosten für Spargel durch \( K_{M}(x)=2,5 x \) beschreiben. Erklären Sie die Bedeutung der Zahl 2,5.
d) Beschreiben Sie in eigenen Worten, wie sich der Graph der Funktion \( K_{5} \) ändert, wenn der Supermarkt eine Spargel-Aktionswoche hat und der Kilopreis sich verringert.
e) Beschreiben Sie, wie sich der Graph von \( K_{B} \) verändert, wenn man zur Hinfahrt die Bahn benutzt, bei der Rückfahrt aber von einem Freund kostenfrei mitgenommen wird.
f) Berechnen Sie, ab welcher Menge es sich lohnt, zum Bauern zu fahren.
Ansatz/Problem:
bei Punkt a) komme ich zwar auf die richtige Funktionsgleichung Ks=5,98x aber warum Kb=2x+6 sein soll weiß ich nicht.
Dass der Achsenabschnitt 6 ist weiß ich. Aber warum ist die Steigung 2?