Hallo HJ,
ich gehe davon aus, dass der rechte Winkel bei C liegen soll.
Sei C = (x|y)
G1 | [1, -2] - [x, y] | = | [5, 1] - [x, y] | (Dreieck gleichschenklig)
√(x2 - 10·x + y2 - 2·y + 26) = √(x2 - 2·x + y2 + 4·y + 5)
x2 - 10·x + y2 - 2·y + 26 - (x2 - 2·x + y2 + 4·y + 5) = 0
8·x + 6·y = 21 → y = - 4/3 x + 7/3
G2 ( [1, -2] - [x, y] ) · ( [5, 1] - [x, y] ) = 0 (rechter Winkel bei (x|y)
x2 - 6·x + y2 + y = -3
y in G2 einsetzen:
x2 - 6·x + (- 4/3·x + 7/2)2 + (- 4/3·x + 7/2) = -3
100·x2 - 600·x + 675 = 0
4·x2 - 24·x + 27 = 0
x2 - 6x + 27/4 = 0
x2 + px + q = 0
pq-Formel: p = - 6 ; q = 27/4
x1,2 = - p/2 ± \(\sqrt{(p/2)^2 - q}\)
x1 = 9/2 ; x2 = 3/2 → y1 = - 5/2 ; y2 = 3/2
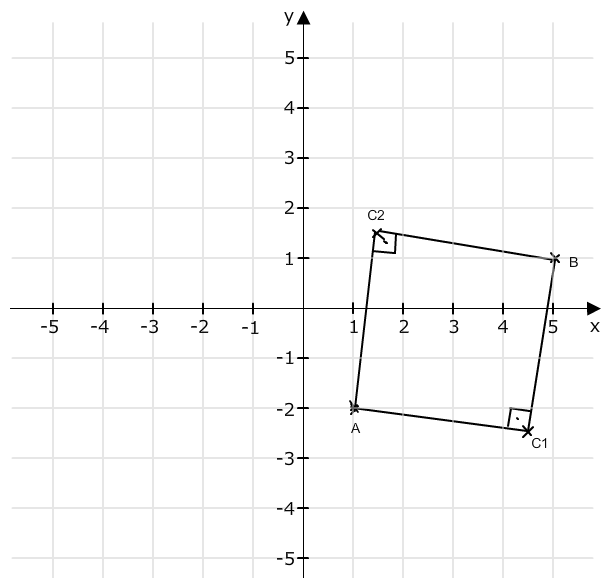
Gesuchte Punkte: C1 ( 9/2 | - 5/2 ) und C2 ( 3/2 | 3/2 )
Gruß Wolfgang