Ich habe ein Problem bei dieser Aufgabe:
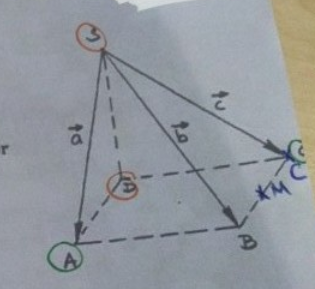
$$\text{Vorgegeben ist eine Pyramide mit quadratischer Grundfläche.}\\ a) \text{Drücke die Vektoren } \vec{AC} \text{ und }\vec{DS} \text{ durch } \vec{a}, \vec{b} \text{ und } \vec{c}\text{ aus }.\\ b) \text{M sei die Mitte der Strecke BC. Drücke den Vektor } \vec{AM} \text{ durch } \vec{a}, \vec{b} \text{ und } \vec{c}\text{ aus }.$$
Ich habe zwar die Lösungen für alle Aufgaben, aber ich verstehe nicht genau, wie man bei der 1a) auf das Ergebnis vom Vektor DS kommt, kann mir das bitte jemand erklären?
Und bem Aufgabenteil b) verstehe ich nicht, wie man den Punkt M berechnet und, wie man auf die Gleichung kommt.
Mein Ansatz:
\( \overrightarrow{A C}=-\vec{a}+\vec{c} \)
\( \overrightarrow{D S}=-\vec{a}+\vec{b}-\vec{c} \quad \) ?
b) \( \overrightarrow{A M}=-\vec{a}+\frac{1}{2} \vec{b}+\frac{1}{2} \vec{c} \)?
Wie bestimmt man M?
Vielen Dank für die Erklärungen.