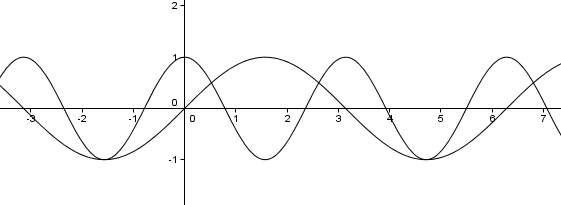
f(x) wird hier nicht direkt durch einen Funktionsterm, sondern durch eine andere Funktion definiert: man erhält f(x), wenn man in g(x) für x einfach 2x+π/2 einsetzt.
Also:
f(x) = g(2x + π/2) = sin(2x+π/2)
Um die Funktion zu zeichnen, kannst du nun entweder einfach Werte für x einsetzen und so Punkte der Funktion berechnen, die du dann verbindest, oder du überlegst dir, was diese "Transformation des Arguments" (Transformation bedeutet Veränderung) bedeutet.
Das +π/2 bewirkt eine Verschiebung der Funktion nach links, denn wenn x = 0 gilt, dann ist f(x) bereits sin(π/2) also ein Wert von weiter rechts.
Das 2x beschleunigt das Fortschreiten auf der x-Achse: geht man um π/2 weiter, dann ist das so, wie wenn man beim sin(x) um π weitergeht. Also geht die Funktion schneller hin und her, man sagt: die Frequenz ist doppelt so hoch.
Die Funktion schneidet die y-Achse also bei (0, 1) und hat dann schon bei π/4 ihre erste Nullstelle.