Wie berechne ich die Mantelfläche einer scheinbar unregelmäßigen schiefen quadratischen Pyramide?

Question

Hi,

Also ich muss die Oberfläche einer Pyramide berechne und ich habe einpaar Probleme/Fragen zu dieser Aufgabe?

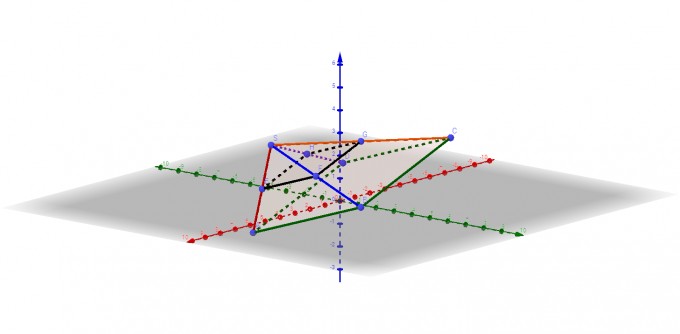
Mir waren Koordinaten eines Pyramidenstumpf gegeben gewesen und ich musste auch die Koordinaten der Spitzen berechnen, dass konnte ich einfach machen.[A(7,1,0); B(7,7,2); C(1,7,4); D(1,1,2),E,F,G,H; S(7,2,4)].

Um die Oberfläche zu berechnen, gilt ja die Formel O=G+M. G habe ich schon berechnet G=a²= (2√10) ² =40, doch bei der Berechnung bei M habe ich Probleme, weil die Formel M=2·a·h_a  kann man doch nicht anwenden, wenn alle Seitenkante s verschieden lang sind und somit auch alle Flächen unterschiedliche h_a Größen hätten.

Denn ich habe die einzelnen Seitenkanten berechnet(Vektoren →):

SA =(7-7, 1-2, 0-4)=(0,-1, -4)

Betrag: ΙSAΙ=√17≈4,123..

SB=(7-7 ,7-2, 2-4)=(0, 5, -2)

Betrag:ΙSBΙ=√29 ≈5,385..

SC=(1-7, 7-2, 4-4) =(-6, 5, 0)

Betrag:ΙSCΙ=√61 ≈7,810..

SD=(1-7, 1-2, 2-4)=(-6, -1, -2)

Betrag:ΙSDΙ=√41≈6,403..

und die sind alle unterschiedlich.

Also ich habe h_a =√(h² +(a/2)² )=√((√11) ² +((2√10)/2)² )=√21 berechnet und das dann in die Formel M=2·a·h_a =2·(2√10)·√21=4√210 ≈ 57,965...eingesetzt.

O=G+M=40+4√210≈97,965...

Also ich wunder mich einfach ob man diese Formel bei so einer schiefen und unregelmäßigen Pyramide benutzen darf und ob meine Rechnungen und mein Endergebnis richtig sind/ist?! Vielleicht bin ich auch ganz dumm und übersehe etwas wichtiges hier, ich entschuldige mich im Voraus, falls das eine total dumme Frage ist!

und ich hoffe mir kann jemand hierbei helfen.

Comments

Die Seitendreiecke einer schiefen quadratischen Pyramide sind im allgemeinen weder deckungsgleich noch gleichschenklig. Die Spitze liegt auch nicht über dem Mittelpunkt der Grundfläche. De Volumenformel wird dadurch nicht in Frage gestellt, aber die Oberflächenformel schon, denn die Seitendreiecke müssen nun ganz anders berechnet werden.

Vielleicht ist es nützlich, die ursprüngliche Aufgabe noch zu ergänzen.

Answer 1

Bei schiefen Pyradiden hat jede Dreiecksseite hat eine eigene Fläche, die man aus den drei Seitenlängen mit der Formel von Heron berechnen kann. Natürlich ist das aufwändig.

"Mir waren Koordinaten eines Pyramidenstumpf gegeben gewesen und ich musste auch die Koordinaten der Spitzen berechnen".

Was sind denn die "Spitzen" eines Pyramidenstumpfes? Wie kann man E, F, G und H bestimmen, ohne die Höhe des Stumpfes zu kennen?

Geht es um eine Pyramide oder um einen Pyramidenstumpf?

Wenn ABCD die Grundfläche der Pyramide ist, welche Form hat ABCD?

Comments

"Geht es um eine Pyramide oder um einen Pyramidenstumpf?"

Also es geht jetzt um eine Pyramide. 

"Wenn ABCD die Grundfläche der Pyramide ist, welche Form hat ABCD? "

Quadrat!?

Also ich habe zwar noch nie was vom Satz des Heron gehört, doch ich habe mir das mal angeguckt und mit den Formel jetzt jede einzelne Seite ausgerechnet und dann die Oberfläche:

A₁ : a= ΙBSΙ =√29; b= ΙASΙ = √17; s= ΙABΙ =2 √10

s=(a+b+c) : 2

s≈7,92

A= √(s· (s-a)· (a-b) ·(s-c))= 11,04 LE²

^A₂ :  b=ΙCSΙ =√61; c=ΙBSΙ=√29; s=ΙBCΙ=2 √10

s=9,76

A=16,91 LE² 

A₃ : c=ΙDSΙ=√41; d=ΙCSΙ=√61; s=ΙCDΙ=2√10

s=10,27

A=19,63 LE² 

A4 : d=ΙASΙ=√17; a=ΙDSΙ=√41; s=ΙDAΙ=2√10

s=8,43

A=12,45 LE² 

^M=A₁ ^+A₂ ^+A₃ ^+A₄ =60,03

^{O=G+M   =40+60,03   =100,03
Wäre das dann so richtig?} 

---

Offenbar bist du dir nicht sicher, ob die Grundfläche ein Quadrat ist. Wenn sie ein Quadrat ist, müssten immer zwei Seiten das Skalarprodukt 0 haben. Ist das so? Da eine Seite der vielleicht quadratischen Grundfläche  10√2 ist, müsste die Grundfläche allein schon 200 sein und die Summe der Seitenflächen (der Mantel) müsste >200 sein.

---

10√2 ist keiner der seiten lang. sondern 2√10? Die Grundfläche hat doch gleich lange Seiten. Also muss das doch  ein Quadrat sein.

---

Ein Viereck mit gleichlangen Seiten kann auch eine Raute sein, die kein Quadrat ist. Aber 2√10 hast du recht. Da hatte ich einen Zahledreher.

---

Ok kein Problem und achso, ich habe geprüft ob es ein Quadrat ; doch es ist kein s, wie du angedeutet hast, eine Raute.

Somit änder sich natürlich das Ergebnis

Ich habe die Grundfläche neu ausgerechnet und dann mit der Mantelfläche addiert O≈100.

Viel Dank fürs helfen.