Der Leuchtturm kann zur Positions-Bestimmung auch zweimal angespeilt werden.

Question

ODer Leuchtturm kann zur Positions-Bestimmung auch zweimal angespeilt werden. Wie weit ist das Schiff bei der zweiten Peilung vom Leuchturm entfernt ? Beschreibe deinen Lösungsweg. Ä

Comments

Aufgabe 2 bitte nur. Danke LG Steven

Answer 1

α = 46 °
β = 180 - 56 = 124 °
γ = 180 - 46 ° - 124 ° = 10 °
c = 2 sm

2.Peilung Strecke a

sin ( γ ) / c = sin ( α ) / a

sin ( 10 ) / 2 = sin ( 46 ) / a
a = 8.29 sm

Comments

Riesen Dank für die schnelle Antwort LG Steven

---

@Georg: Der Winkel bei der 2.Peilung ist 58° nicht 56°.

---

@steven_james,
  gern geschehen.
Falls du weitere Fragen hast dann stelle
sie wieder ein.

Ansosnten : worauf Werner hingewiesen hat.
Der Winkel ist 58 °. Bitte entsprechend korrigieren.

---

Dies ist Aufgabe 2., der Sinussatz wird aber erst nach Aufgabe 3. hergeleitet und formuliert.
Die Frage mag daher erlaubt sein, ob seine unkommentierte Anwendung hier vom Aufgabensteller intendiert war.

Answer 2

zeichne in dem Dreieck, welches aus den beiden Schiffspositionen \(P_1\) und \(P_2\) und dem Leuchtturm \(L\) gebildet wird, den Winkel am Leuchtturm ein (grün):

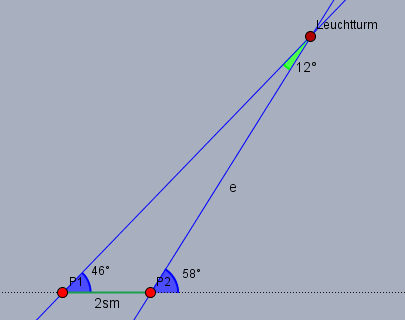
Der Wert des grünen Winkels folgt aus der Summe der Winkel im Dreieck und beträgt \(12°\). Dann kann man die Seite \(e\) - also die Strecke \(P_2L\) - nach dem Sinussatz berechnen. Es gilt:

$$\frac{e}{\sin(46°)} = \frac{2 \text{sm}}{\sin(12°)} \quad \Rightarrow e = \sin(46°) \frac{2 \text{sm}}{\sin(12°)} \approx 6,92 \text{sm}$$

Gruß Werner

Comments

Bedanke mich für die ausführlichere erklärung von ihnen, hab es jetzt noch viel besser verstanden Damkeeee ! :D