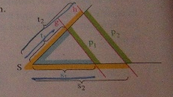
Bitte helft mir !! Rechnet mir die aufgaben bitte aus und erklärt sie kommen nicht weiter !!!! Bitte 7a+b !!!
7. a) Von den vier Längen s1, s2, t1 und t2 sind drei gegeben. Berechne die vierte Länge.
(1) \( s_{1}=3,0 \mathrm{cm} \)
\( s_{2}=7,0 \mathrm{cm} \)
\( t_{1}=4,2 \mathrm{cm} \)
(2) \( s_{1}=2,5 \mathrm{cm} \)
\( t_{2}=3,5 \mathrm{cm} \)
\( s_{2}=4,0 \mathrm{cm} \)
(3) \( s_{1}=4,8 \mathrm{cm} \)
\( t_{1}=5,4 \mathrm{cm} \)
\( t_{2}=7,5 \mathrm{cm} \)
(4) \( t_{1}=5,2 \mathrm{cm} \)
\( t_{2}=9,1 \mathrm{cm} \)
\( s_{2}=6,3 \mathrm{cm} \)
b) Berechne von den sechs Längen s1, s2, t1, t2, p1 und p2 die nicht gegebenen Längen.
(1) \( s_{1}=7,2 \mathrm{cm} \)
\( t_{1}=6,8 \mathrm{cm} \)
\( t_{2}=10,2 \mathrm{cm} \)
\( p_{1}=5,4 \mathrm{cm} \)
(2) \( s_{1} 1=4,8 \mathrm{cm} \)
\( t_{2}=11,0 \mathrm{cm} \)
\( p_{1}=5,4 \mathrm{cm} \)
\( P_{2}=9,9 \mathrm{cm} \)
(3) \( \mathrm{s}_{2}=6,0 \mathrm{cm} \)
\( t_{2}=7,2 \mathrm{cm} \)
\( \mathrm{p}_{1}=4,9 \mathrm{cm} \)
\( \mathrm{p}_{2}=8,4 \mathrm{cm} \)
(4) \( \mathrm{s}_{1}=27 \mathrm{mm} \)
\( s_{2}=4,5 \mathrm{cm} \)
\( t_{1}=3,3 \mathrm{cm} \)
\( \mathrm{p}_{2}=40 \mathrm{mm} \)