Hallo gastek,
Setze die Polarkoordinaten in die Bedingung der Menge ein. Es ist
$$(x^2+y^2)^2 = y(3x^2 - y^2)$$
$$(r^2(t)\cos^2 t + r^2(t)\sin^2 t)^2 = r(t) \sin t (3 r^2(t) \cos^2 t - r^2(t) \sin^2 t)$$
$$r^4(t) = r^3(t) \sin t (3 \cos^2 t - \sin^2 t) =r^3(t) \sin t (3 - 4\sin^2 t) \quad \text da \space \cos^2t = 1 - \sin^2 t $$
Aus \(\sin 3t = 3 \sin t - 4 \sin^3 t\) folgt, dass \(\sin t(3- 4 \sin^2 t) = \sin 3t\) ist. Dies Einsetzen und nach Division durch \(r^3(t)\) erhält man
$$r(t) = \sin 3t$$
Und so sieht die Kurve aus $$M = \{\left(x(t),y(t)\right)^T \in \mathbb{R}^2, \space t \in [0 \space .. \space \frac{\pi}{3}]: \\ \quad x(t)=\sin 3t \cdot \cos t, \space y(t) = \sin 3t \cdot \sin t\}$$
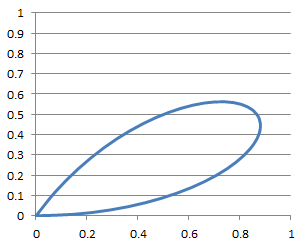
Bleiben noch die Intervalle \(t \in [\frac23\pi \space .. \space \pi]\) und \(t \in [\frac43 \pi \space .. \space \frac53 \pi ]\) zu betrachten. Das sollte jetzt kein Problem mehr sein - oder?