Kurvendiskussion - Nullstellen

Question

hallo erstmal! 

F(x) = 1/15 x ^4 - 1/15 x ^3 - 16/15 x ^2 + 14/15 x + 37/15

Kann mir Jette jemand helfen die nullstellen dieser Gleichung zu errechnen.

eure annika !!

Answer 1

Hallo Anni,

F(x) = 1/15 x⁴ - 1/15 x³ - 16/15 x² + 14/15 x + 37/15 = 0   | * 15

⇔  x⁴ - x³ - 16·x² + 14·x + 37  =  0

[ Die Rechnerlösungen sind

    x₁ = -3,66094636  ;  x₂ = - 1,22331011 ; x₃ = 2,314136625  ;  x₄ = 3,57011985 ]  

Die Gleichung hat also keine Lösungen, die man durch Probieren finden kann (ganzzahlig kämen nur die Teiler ±1 und ±37 des konstanten Summanden 37 infrage. 

Man benutzt dann meist ein Näherungsverfahren, z. B. das

Newtonverfahren:

 Berechnen der Nullstellen von f(x)  (f muss differenzierbar sein) 

hier:  f(x) = x⁴ - x³ - 16·x² + 14·x + 37  

         f '(x) = 4·x³ - 3·x² - 32·x + 14

Ausgehend von einem (möglichst guten) Startwert, den man z.B zwischen zwei x-Werten findet, deren Funktionswerte verschiedenes Vorzeichen haben, findet man - auch mit einem einfachen Taschenrechner -  immer bessere Werte mit der Formel

x_neu =  x_alt - f(x_alt) / f ' (x_alt)

Du weißt allerdings i.A. nicht, ob du alle NS gefunden hast.

Manchmal konvergiert das Verfahren nicht (wenn du für x_alt zum Beispiel eine  Extremstelle erwischt). Dann hilft oft ein anderer Startwert.

Je besser der Startwert, desto weniger Rechnung:

mit Startwert 1 ergibt sich z.B.

x	f(x)	f '(x)
1	35	15
-1,333333333	-4,580246914	41,85185185
-1,223893805	-0,024127368	41,33769295
-1,22331014	-1,13927E-06	41,33378708
-1,223310113	0	41,3337869

mit Startwert 2:

x	f(x)	f '(x)
2	9	34
1,735294118	16,95639046	-29,66156116
2,306956221	0,191089873	-26,67782229
2,314119095	0,000465373	-26,54745916
2,314136625	2,82363E-09	-26,547137
2,314136625	0	-26,547137

Wenn ein Plotterbild zur Verfügung steht, findet man natürlich leicht gute Startwerte:

 
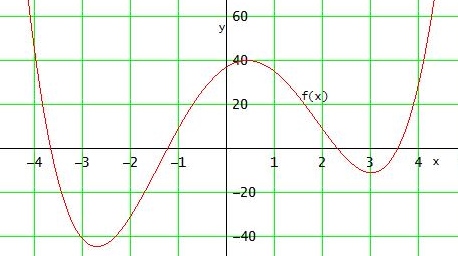
Aber auch "schlechte" Startwerte liefern Ergebnisse, z.B.:

x	f(x)	f '(x)
100	98841437	3970014
75,10300039	31302022,1	1675151,401
56,41691502	9900983,948	706930,4953
42,41131756	3130958,286	298404,9945
31,91900562	989663,0269	126015,3811
24,06549585	312582,5722	53256,40373
18,19610644	98595,5504	22537,22859
13,82132051	31025,8053	9559,717694
10,57584755	9722,690259	4071,600136
8,187918986	3024,656068	1746,598966
6,456178542	928,7718911	758,7875319
5,232157519	278,4263491	337,3756756
4,406886555	79,54304039	157,0560727
3,900423869	20,29937956	80,89989014
3,649504127	3,776237329	51,68846241
3,576446482	0,277421281	44,16567491
3,570165105	0,001970139	43,53890413
3,570119855	1,01898E-07	43,53440038
3,570119852	0	43,53440014

Gruß Wolfgang

Comments

Wow super vielen Dank für die umfassende super gut beschriebene und vorallem schnelle Rückmeldung! 

Hat mir sehr geholfen!