Hallo Benis,
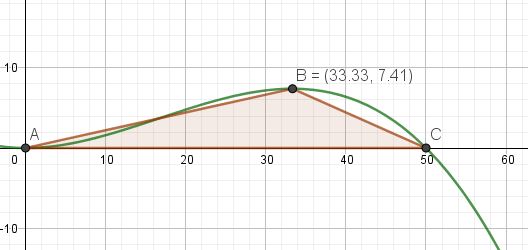
wenn du bei den Deichquerschnitten den Hochpunkt als Punkt eines Dreiecks nimmst, dessen Grundseite 50 m ist, kannst du den Flächeninhalt des Dreiecks berechnen und mit 1 km bzw. 1.000 m multiplizieren. Das ergibt 185.250 m^3 und aufgerundet 200.000 m^3.
Die Antwort zur zweiten Aufgabe schicke ich gleich.
Gruß
Silvia